|
|
The Farben Project
retuning to Nature & scalar
coloration
music & psycho-acoustics
|
Intro &
Definitions
§ 1 Musical Sound
§ 2 The Tone
§ 3 Naturalizing
Master Pitch
§ 4 Color Spectrum
and Pitch
§ 5 The Harmonic
Series
§ 6 Defining Tonal
Scales
§ 7 The Tuning System
§ 8 Psycho-Acoustic
Definitions
Introduction & Definitions
In "Farben Project", the
German word "Farbe" ("color") refers to
"Klangfarbenmelodie", a musical technique involving splitting
a melody between several instruments, rather than assigning it to
just one instrument (or set of instruments). The aim was to add
color (timbre) and therefore alternative texture to the melodic
line. This technique derives from Arnold Schoenberg and his
"timbre-structures" and was also used by Anton Webern.
With the "Farben Project", my first aim is to integrate
color into
music and this by three methods : (a) aligning standard pitch with
natural process, (b) relating the chromatic scale (and on the basis
of this also the harmonic series of each tone) to the visible
spectrum of light and (c) allowing scalar coloration, or the return
of "key characteristics" to the 24 keys of the tonal system of
harmony (by reintroducing pure intervals). Secondly, on the basis of
this naturalization and reintroducion of scalar coloration, define a
psycho-acoustic model, in other words, establish guidelines allowing
music to entrain the minds of its listeners (AVS) in the
direction of a life more in harmony with the beauty of the
natural order.
Music, derived from the Greek "mousike" or "art of the
Muses", is an artistic phenomenon whose medium is well-formed sound
in combination with its absence (silence). This definition of music
begs the question : "What is art ?", a topic involving a complex
network of concepts studied in
Aesthetics
(2013).
Three ways to define "music" can be identified : (1) intrinsic, (2)
(inter)subjective and (3) intentional.
• Intrinsic, objectivist definitions try to pinpoint the objective
aural properties of musical sound as opposed to mere noise, for
example specific frequencies. But if we want to include
"out-of-tune" sound-sources (like machines), different Western &
non-Western musical (microtonal) scales, "untuned" percussion and
works lacking basic "musical" features (such as pitch or rhythm)
-like Yoko Ono's Toilet Piece/Unknown- then the intrinsic
definition becomes too extended, for indeed both non-musical noise
and musical sounds have frequency. However, it cannot be denied
"music" has certain "musical" properties, of which frequency (pitch)
and temporal pulse (rhythm) are the most basic, and this together
with dynamics (loudness, intensity), timbre (tone-color),
verticality (harmony), horizontality (melody, counterpoint) and
format.
• (Inter)subjective definitions identify music, regardless of
intrinsic properties, as whatever sounds like or is perceived by a
listener or a group of listeners as music. Can one say Beethoven's
Fifth Symphony stops being music for listeners ignorant of
Western culture ? Can I reasonably deny Rembrandt's The Night
Watch to be a painting ? Can I miraculously transform the noise
of a drilling machine into music by merely hearing them in a certain
way ? And what about music emitted by a radio nobody is attending ?
Does this stops being music (while it remains music for the
neighbour next door) ? Clearly all of this is counterintuitive. Too
much subjectivism (like exclusive objectivism) leads to problems.
• Intentional definitions focus on music-making intentions of those
responsible for the noises or sounds. Not the listener is important,
but the intent of the human sound-source. Intentional action has
been defined as "the execution and realization
of a plan, where the agent effectively follows and is guided by the
plan in performing actions which, in manifesting sufficient levels
of skill and control, bring about the intented (i.e. planned)
outcome." (Livingston,
2005, p.14). This definition helps to include works of silence, like
John Cage's work 4'33". So-called music produced by machines
(CD players, iPods, etc.) is rooted in the intentions of the
musicians behind the sounds. Even computer-generated scores are
designed by someone, even if the outcome is unpredictable. The same
goes for aleatoric music (or passages) and improvisations. So these
are covered by the definition. Sounds generated by animals however,
although they sound like music, lack the capacity for complex
intentions and so do not improvise or invent new melodies. These
sounds fall outside the definition. They are music-like without
actually being music.
In the definition of
what is music, both intrinsic & intentional approaches will be
combined. From the intrinsic strategy we retain the presence of
objective musical features. This begs the question : What are
objective musical features ? From the intentional approach, the
importance of a human source for acoustic events is adopted. An
extended & strict form of the definition is proposed. In sensu
lato, all types of sound (combined with silence) are allowed,
whereas in sensu stricto, only well-formed sounds are taken
into account.
• Extended definition of music :
Music is any event
intentionally produced to be heard, either to possess intrinsic
musical features or to be listened to for such features.
By saying "any event intended to be heard", the definition includes
both sound & silence. If we want to include machine-noise etc.
intended to be part of a musical work (like Honegger's Pacific
231), then the musical event is not limited to well-formed
sound. The disjunction in the definition allows one to call works
like Toilet Piece/Unknown "musical" for indeed the toilet is
flushed with the intent to discover musical features, even if
such features are objectively lacking (but projected upon the
acoustic phenomenon by intent). According to this definition, some
sonic works of art are not musical in any way (cf. John Cage's
Williams Mix for eight simultaneously played independent
quarter-inch magnetic tapes). Hence, not all sound art is music !
• Strict definition of music :
Music is a well-formed sound
(combined with silence), intentionally produced to be heard.
The restriction here is the condition of well-formedness,
excluding all sonic works of art lacking all or some intrinsic
musical features such as pitch, rhythm, dynamics, timbre, melody,
harmony & format. Unpitched instruments form an exception, and may
be included, but only in combination with pitched instruments. A
sonic artwork exclusively generated by unpitched instruments is
excluded. So is Toilet Piece/Unknown, despite Yoko Ono's
intent, as well as Cage's 4'33". This definition includes
Western & non-Western sonic works making use of microtonality
(Indian Râgas, works of Harry Partch). If the concept of
well-formedness is stretched to include pitched or unpitched noise
(like that produced by machines, trains, traffic etc.), then music
is at hand if and only if this noise is combined with less
random (read : more traditional) sources of sound (like musical
instruments). In this case, the overall balance between noise &
sound needs to be checked in order to know whether music is at hand
or not.
§ 1 Musical
Sound
There are two types of
sound : musical sound & noise. Let this crucial initial distinction
be rooted in the physical (material, efficient) difference between
irregular & regular sound waves.
Everything around us, our body included, vibrates in a certain
pattern and transfers these vibrations to the surrounding medium.
When these vibrations disturb the medium in a periodic way, a
portion is repeated over and over again, i.e. with repetitions at
equal time intervals. One cycle of this periodic motion is called a
wave, characterized by a high point (crest) and a low point
(trough).
Sound is a longitudinal wave, i.e. an oscillation of pressure
transmitted through a medium (like air or water) causing the
particles in the medium to vibrate parallel to the direction
in which the wave is travelling, and composed of frequencies within the range of hearing. The speed of sound is proportional
to the square root of the ratio of the stiffness of the medium to
its density. In dry air at 20° C (68 °F), the speed of sound is
343.2 metres per second (1.126 ft/s), or about a kilometre in three
seconds (a mile in five seconds). The moment musical is a
single temporal unit not exceeding three seconds, the time span of
immediate consciousness. This is the specious present, the
time duration wherein one's perceptions are considered to be in
the present. In this moment, earlier may be distinguished from
what is later, but both past & future are directly given,
simultaneously present to consciousness. So the "present", events
perceived in the first time, is not merely a non-existent gap
between before and after.
When an object vibrates, waves of
increased and decreased pressure in the air are caused. It is not
the case of a particular molecule of air moving in the direction of
the wave at this speed. Rather, the local disturbance to the
pressure propagates at this speed. This is similar to water. No
particular piece of water moves along, but the disturbance of the
surface propagates. However, in the latter case the local movements
are up and down, and so at right angles to the direction of
propagation (transverse waves). Sound moves in the same direction as
the propagation (longitudinal waves).
A sound wave travels through the air, hits the eardrum and allows
one to hear the sound. Human hearing is normally limited to
frequencies between about 20 Hz and 20.000 Hz.
Compare this with a turtle (20 - 1000 Hz), a dog (50 - 45.000 Hz), a
cat (30 - 50.000 Hz) and a dolphin (1000 - 130.000 Hz). The human
ear can distinguish a difference of 1 - 2 Hz.
Sound waves (and waves in general) are characterized by frequency,
amplitude, wavelength & period. The frequency (f) is the number of waves
passing a given point per second and measured in Hertz (Hz), with 1
Hz = 1 vibration/second. The amplitude (A) of a wave is the
maximum displacement from the equilibrium position (the original
position of the sounding body). The wavelength (λ) is the distance
between any point on the wave and the corresponding point on the
next one (or the distance the wave travels in one cycle). The period
(T) is the time it takes for one whole cycle to pass a given point.
Period & frequency are reciprocals, with T = 1/f.
A sonic environment is composed of many different sound waves
emitted by a variety of sound sources. Interacting, they usually
produce
irregular sound-ripples, causing a cacophony. This mixture of
sounds is discordant & harsh. It is generated by vibrations producing
irregular sound-ripples. These complex
pressure ripples have no or little relationship to each other
and therefore clash. Instead of co-operating, as in a team, they as
it were "beat each other up", increasing the irregularity of their
interactions. Irregular sound waves are never well-formed. Hence
they are called "noise".
|
sound waves in a sonic environment |
regular ripples |
musical sound |
uncommon |
cultural |
|
irregular ripples |
noise |
common |
natural, cultural |
In the common aural
chaos surrounding us, regular sound-ripples are very noticable, they
stand out, are uncommon. Always working together, these waves
reinforce each other, and generate strong resonance in any sonic
environment. When, as in a musical performance, surrounded by total
silence, these regular sound waves immediately reveal their
exceptional status. But in the sonic environment, these well-formed
sounds constitute but a small subset of all possible sounds.
And to generate these musical sound waves special tools are
necessary. Although music imitates (cf. the Harmonic Series)
fundamental natural phenomena (like φ), these sound waves are always
the symptom of a degree of culture accommodating the production of
cultural forms, in casu, musical works of art, the first of
which were very likely composed ca.30.000 BCE (date of the oldest
instruments -
Davies,
2014, p.70).
So music can be understood as a finite number of musical
sounds
generating regular sound-ripples interacting & working
together to produce an organized and hence well-formed
sound. The objective musical features or attributes are therefore
certain phenomena contributing to a musical sensation as
opposed to other aural sensations, such as sonic works of art using
noise & various degrees of noise.
The history of music around the globe evidences seven musical
features denoting music in objective terms : pitch, rhythm,
dynamics, timbre, horizontality (melody, counterpoint), verticality
(harmony) and format (musical architecture, overall layout or plan
of a piece). Together, these seven intrinsic features define music
as an objective, sounding form (cf.
Hanslick's
"tönend bewegte Formen"). This as opposed to noise, or unmusical
sound.
Of these seven objective features, two are fundamental : pitch &
rhythm. Pitch is fundamental, for it is the qualitative attribute of
auditory sensation denoting highness or lowness primarily
conditioned on the frequency of sound waves. We do not hear
this rate of vibration of musical sound waves, but only a "musical
tone". Pitch determines spatial organization. Next comes
temporal motility, defining the durations of pitches, known
in music as rhythm (tempo, time). With both, the foundational
spatio-temporal sphere of music is set. Loudness speaks of the
intensity of certain sound waves relative to others, whereas timbre
is a function of the instruments generating the musical sound. The
horizontal, vertical and integral features are meta-properties based
on the distribution of pitch, rhythm, dynamics & timbre. Format
is called "integral" because it involves the organized layout of all
the musical events constituting a work of music.
Well-formed sound (and its absence, silence) are the medium of
music. The musical phenomenon is an object of human valuation
fulfilling specific determined aims. Its conscious perception (acoustic &
kinesthetic) -as well as music's unconscious impact on the whole body
through resonance- leads towards the elaboration of conjectured meanings,
in casu : what is a well-formed sound ? Music is an intentional
phenomenon. It is the object of human valuation because it belongs
to the interests of an individual, a group or humanity as a whole to
define what is music and what it is not.
Let us focus on pitch, the most objective of the intrinsic
properties of music.
§ 2 The Tone
In music theory, the
word "note" refers to a sign, say G, calling for pitch (frequency), relative loudness (amplitude),
duration (rhythm) & timbre (quality or shape of the
frequency spectrum of the sound wave). In acoustics, G implies a
pitched musical sound, i.e. a specific steady periodic
oscillation called "tone". As a note, G always calls for a
functional discussion about its relationship with other notes. The
note G is the tonic in the key of G or g, the mediant in E or e and
the dominant in C. In each case, for the same G, another functional
relationship with the other notes of the scale is given. The concept
"note" is therefore contextual. G as a tone is just a matter of
frequency, and this independent of context.
Pitch, rhythm, loudness & timbre are the fundamental dimensions of
the single sounding tone. They answer the four questions denoting the
primary features of its sound wave, related to its physical
existence :
(1) spatial : how high or low is the frequency ?
(2) temporal : how long is the frequency operational ?
(3) intensity : how strong, how much
energy carries the frequency ?
(4) timbre : which instrument generates the frequency ?
The common element is frequency, the number of waves passing
a given point per second (in Hz). When tones are combined, the
meta-dimensions come in : harmony, counterpoint & format. Tones may sound
simultaneously, generating a vertical relationship
(harmony), or one after the other, inviting a horizontal
dialogue (melody and by extension counterpoint).
Finally, format defines layout and plan. This is the last dimension
: architecture. All together they define an actual musical form
existing in the moment musical.
In musical practice, secondary frequency features are also present, such
as attack transients (high amplitude, short-duration sound at the
beginning of the wave), vibrato (a musical effect consisting of a
regular, pulsating change of pitch), envelope modulation (the
so-called ADSR-factor, or the "Attack
Decay Sustain Release" specifics of an instrument) and reverb (impact
of performance space on the sound). They are used with great care &
moderation.
Sounding a single tone is not yet music, but merely the most
elementary building-stone of music, a
well-formed sound generated with vibrations collaborating to produce
a regularly repeating sound-ripple, i.e. vibrations strongly related to
each other and joining together in an organized way. The most
forward way to generate a single tone is making a single string
(monochord) vibrate or a column of air do the same.
All musical
tones, besides electronically generated "pure" tones, are
complex,
i.e. formed by adding an infinite number of component waves, each having a
different frequency. This infinite set of frequencies is
divided into two : the fundamental frequency and the others. The
fundamental is the dominant frequency, the one best heard and
somewhat overpowering the others. These are always integer multiples
of the dominant frequency.
A musical tone consists of a
fundamental frequency component plus other frequency
components (in "pure" tones, only the fundamental frequency is
present). These frequency components (fundamental + other frequency
components) are called "partials" (or "parts" of the
total, infinite spectrum of frequencies constituting a musical tone). The xth partial of
a tone is the xth frequency component counted from the bottom. So the
first partial, the one with the smallest frequency, is the fundamental frequency or fundamental (f) of the
tone. All frequency components besides the fundamental frequency
(first partial) are "overtones" ; they never include the fundamental
frequency.
As the frequencies of the overtones of a tone are integer multiples of
its fundamental frequency (2f, 3f, 4f, ...), order & balance is
evidenced and so all partials (all frequency components) are called "harmonics"
; the fundamental frequency being the first harmonic. The component
with frequency xf is called the xth harmonic or (x - 1)th overtone.
With x = 1, we obtain the first harmonic (= first partial), i.e. the
fundamental. There is no overtone (x = 1 - 1 = 0). The first overtone is
the second harmonic or the second partial. With x = 3, we
obtain the 3th harmonic or second overtone. Simply put : overtones =
harmonic - 1 and so harmonics = overtones + 1. The series of
harmonics, from the first harmonic up to the xth harmonic is called
the Harmonic Series. In theory, an infinite number of harmonics
exist, but in practice the first sixteen harmonics are considered,
of which the first six are crucial to tone-formation and vertical
(simultaneous) interactions between tones (harmony).
When the totality of the frequency spectrum of a tone is at hand the
term "harmonics" will be used (as in acoustics), but when the
dominant influence of the fundamental frequency is considered,
"overtones" are indicated (as in sound engineering).
From the physical point of view, musical sounds are "musical"
because these pitches have regular ripple-patterns. This
regularity is obvious, for all frequency components besides the
fundamental component are integer multiples of the latter. Of
all the frequency components of a tone, the fundamental frequency,
first harmonic or first partial is the dominant frequency.
From the informational & sentient perspective, "music" also operates
the other six dimensions besides pitch, namely duration, tone
quality (sonance), verticality, horizontality and integrality. Let
it be clear sound waves with irregular ripple-patterns or noise lack this
harmonic feature. Noise is inharmonic. All the frequencies of a
single musical tone or pitch are in "harmony", i.e. work together in
a unity promoting difference.
The fundamental frequency defines the foundation of a tone,
but also contains overtones (the fourth & the fifth) generating
the basic structure of the triadic relationships at work in
verticality (tonal harmony). The Harmonic Series of C contains E
& G, forming the tonic triad of C Major.

Harmonic
Series of C (with offset in cents, 1 octave = 1200 cents)
When the frequencies of the partials are
not integer
multiples of the fundamental frequency, an inharmonic is at
hand. When a violin plays a tone, the vibrating string is made up of
its individual harmonics coming together as "one". But when the
string is plucked or struck, it exhibits inharmonicity. At
that moment, the
sound waves do not blend together, and small irregular ripple-patterns
occur (often of very short duration). In the strict definition of
music, inharmonic tones are not the rule. Music is primarily based on tones with a
well-balanced Harmonic Series (a set of blending harmonics). The "common use" of noise in
Western music may punctuate rhythm or be called in to
put in sharp contrast, loud accentuation or climax. But such inharmonicity, in terms of the strict
definition of music, is always used sparingly. In the extended
definition, inharmonicity may be a prime component of music, or be
part of elaborated & recurrent aleatoric devices ...
Two
tones with the same fundamental frequency are in unison and
totally
blend together, producing a fusion with no interference between them.
In general terms, when two
sound waves interfere, they sometimes combine, making a louder
sound, and sometimes partially or fully cancel each other out,
producing
a softer sound. This pulsating pattern of louds & softs is called
beats. For example, given sound wave X has a pitch of 50 Hz and
sound wave X' a
pitch of 55 Hz, then 5 beats per second are heard. Now when the
pitch of one of two tones of the same fundamental frequency is slightly
increased, then the number of beats heard per second also increases,
creating discord. Maximum discord or dissonance is generated when
the beat frequency (the difference between the two fundamental
frequencies) is about 25 or 30 Hz. Beyond that, this decreases, to
finally disappear.
When one tone has a fundamental frequency
double that of another tone, they form an octave and no beats are heard
either. Unison & octave are the two universally recognized fundamental
consonant intervals between
two tones. Defining other tone-relationships than unison & octave is
answering the question of how to divide the octave. This is another
crucial initial distinction.
"Accordingly, in all known tonal systems, the
basic basic scale-patterns, with few exceptions, fill in the space
between two tones an octave apart." -
Hindemith
(1942, Book 1, p.15).
§ 3 Naturalizing Master Pitch
Is there an absolute way to know whether two
tones played on
a single instrument or two tones played by several instruments
simultaneously are "in
tune" relative to one another ? To answer this, we need to know
the fundamental frequencies of the tones in question. This depends on
the frequencies attributed to them and this is necessarily defined
by a standard. In terms of notation, this means we need to know
which frequencies to attribute to which note.
Put technically, and by consensus, we need to know the fundamental
frequency of A above middle C, the so-called "master tuning" or
"standard pitch". This is the frequency all instruments are set
to (sound this A). This frequency is usually "locked" in a tuning fork, a
relatively stable tuning device invented by John Shore in 1711, and
used to tune instruments before Hertz came along (tuning forks aim
to let the fundamental frequency ring through at the expense of the
other partials). The fact these
forks survive, allow us to reconstruct these historical master
tunings. In the orchestra, the oboe is used to "sound the A"
because this instrument has fixed, factory-tuned tones.
At a conference held in May 1939, the British Standards Institute
endorsed A4 above middle C (C4) to correspond to 440 Hz. One has
only to recall history to realize this was a conventional decision.
In Germany, prior to 1600, organ pitch is thought to have varied
from A at 567 Hz for the first simple pipe organs of the Middle
Ages, to A at 377 Hz for the early modern German organ around 1511.
Handel (1751) favoured A = 422,5 Hz, Mozart (1780) A = 421 Hz (Mendel,
1968).
Scientific pitch, also known as "philosophical pitch" or "Sauveur
pitch", with A = 430,54 Hz, was first proposed in 1713 by French
physicist Joseph Sauveur. Pleyel's piano's (1836) were at A = 446,
Giuseppe Verdi considered A = 432 Hz to be better. In 1859, the
French Government made the "diapason normal" or A = 435 Hz
law, whereas in 1896, Britain adopted "philharmonic pitch" or
A = 439 Hz. In 1925, the American music industry adopted A = 440 Hz.
In November 1955 and in January 1975, the International Organization
for Standardization reaffirmed A = 440 Hz. In 1989, over a dozen of
opera singers -including Placido Domingo & Luciano Pavarotti- added
their names to a petition before the Italian government, asking them
to lower the standard pitch from A = 440 Hz to A = 432 Hz. In their
view, A = 440 Hz is one of the main reasons for the crisis in
singing, giving rise to "hybrid voices" unable to perform the
repertoire assigned to them ... Apparently, the issue of standard
pitch is a fundamental discussion in music.
The objective solution to this problem proposed here is derived
from the structure & function of the human ear, in particular the φ
shape of the outer ear and the cochlea (inner ear), as well as the
function of the latter (cf. φ dampening). The Golden Ratio φ = (1+√5/2)
≈ 1,618033988749894848204586834 ... is part of so many
natural processes it has been called the "Divine proportion".
Indeed, the ratio is expressed in the arrangement of branches along
the stems of plants, in the veins in leaves, in the skeletons of
animals, in the proportions of chemical compounds, in the geometry
of crystals, in the magnetic resonance of spins in cobalt niobate
crystals, in the human genome DNA, etc. In Zeising's Law
(1854), the Golden Ratio permeates all structures, forms and
proportions, whether cosmic or individual, organic or inorganic,
acoustic or optical and finds it full realization in the human form.
φ is also closely related to the Fibonacci numbers (Fn), Fibonacci series
or Fibonacci sequence. These are the numbers in the following
integer sequence Fn : 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
defined by Fn = F(n-1) + F (n-2),
whereas Fn = φn-(-φ)-n/√5.
In the inner ear, the purpose of the φ-shaped cochlea is to separate
out sound into various frequency components before passing it unto
the nerves. This makes the functioning of this body of great
interest in terms of the harmonic content of a single note in
particular, as well as music in general. Can it therefore be mere
coincidence E3 = 161,817 Hz (or φ) when A4 = 432 Hz ? Clearly not.
No other Master Tuning generates φ.
Because A = 432 Hz, or "Verdi Pitch", aligns with φ, this Master
Tuning may be considered an objectivation of standard pitch on the
basis of acoustic law in general and the mechanism of human frequency
processing in particular. These are natural phenomena, not
cultural. Master Tuning A = 432 Hz is therefore the Natural Master
Tuning. When the objective & subjective parameters of acoustics are
not followed (moving away from A = 432 Hz), we interfere with these
natural lines of communication between sound-source &
sound-receptor, thus placing additional stress on the sense of
hearing, and this for reasons beyond those related to the
optimalization of Master Tuning in terms of musical sound. Tones
are always harmonics and our ear differentiates frequencies
on the basis of φ. As we humans are capable of hearing a difference
of 1 to 2 Hz, one cannot claim this matter futile.
Given the Harmonic Series (on the side of the object, the
sound-source) and the hearing apparatus (on the side of the subject,
the sound-receiver, the hearer) are defined by φ, it stands to
reason music should best adopt Verdi Pitch and not some arbitrary
standard facilitating an industry. Given most, if not all, music
today is tuned to A = 440 Hz, we may digitally retune (using quality
software like Melodyne Editor). The fact top singers prefer A = 432
Hz should not be considered whimisical.
§ 4 Color Spectrum and Pitch
"The eye perceives in light which has been split up by a prism a
natural series of vibration frequencies. The light of the sun always
produces the same immutable series of colors, familiar to us in the
rainbow. Now, just as light consists of graduated colors of the
spectrum, so a tone consists of many partial tones. Spectrum of the
world of sound is the harmonic or overtone series. A tone produced
by a voice or instrument carries with it a greater or lesser number
of barely audible overtones. Their order is not arbitrary : it is
determined by a strict law, and is as immutable as the color series
of the rainbow."
Hindemith
(1942, Book 1, p.16).
As the Greeks (following Pythagoras & Plato) considered all
phenomena to be ruled by numbers, the correspondence between
(regular) musical sound (defined by fractions) and the regular
movement of the planets seemed self-evident. Today, this notion of
"music of the spheres" (Musica Universalis), even cherished
by Kepler, may be used as a heuristic tool to help us discover
significant (in a material, information, sentient sense) unexpected
correlations between natural phenomena, in casu, between
visual elements, such as colors, and aural phenomena, such as tones.
Can pitch be related to
color ?
To extend the Pythagorean idea of the "Harmony of the Spheres",
encompassing planets, tones and colors, Plato linked the intervals
of a major second and a perfect fifth to yellow and the perfect
fourth to red. Aristotle also suggested a parallel between the
harmony of colors and the harmony of musical intervals. To directly
attribute color to notes, various systems have come into existence,
either based on an objective measure (Newton in his Opticks,
1704) or on the subjective experience of color. The latter
tradition is based on Goethe (Zur Farbenlehre, 1810).
"Goethe's theory of the origin of the spectrum
isn't a theory of its origin that has proved unsatisfactory ; it is
really not a theory at all. Nothing can be predicted by means of it.
It is, rather, a vague schematic outline, of the sort we find in
James's psychology. There is no experimentum crucis for
Goethe's theory of color." - Wittgenstein, L. :
Bemerkungen über die Farben, 1950.
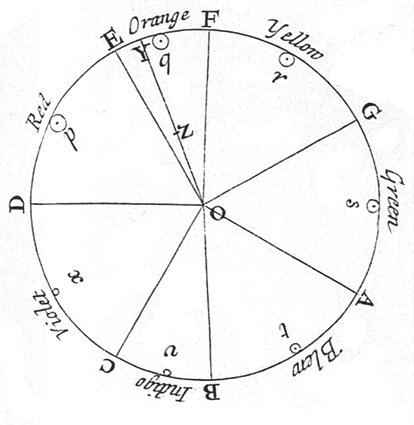
Newton's
Color Circle (Opticks - 1704)
In Newton's circle, the
spectral colors from red to violet are divided by the notes of the
musical scale, starting with D (Dorian). The seven spectral bands are
associated with the seven tones (dividing the octave). The circle completes a full octave,
from D to D. Newton's circle places red, at one end of the spectrum, next
to violet, at the other (non-spectral purple colors are observed when red
and violet light are mixed). Newton's name for "indigo" is what today is
called "blue", whereas his name for "blue" is what today is called "cyan".
Why D is used remains unclear. This, together with the absence of
numerical correspondences between colors & tones (frequency), makes
Newton's scheme somewhat arbitrary.
The question before us : can the notes of the chromatic scale, each
representing a specific tone and therefore frequency, be correlated with
the spectral colors ?
An intriguing numerical correspondence between the pitch or
frequency of the
notes of the chromatic scale & the colors of the visible light
spectrum can indeed be observed. This is the basis of the objective measure
proposed here.
The visible light spectrum is a section of the electromagnetic radiation
spectrum visible to the human eye. It ranges from ca.380 nm (3,8 x 10-7m) to ca.750 nm (7,5
x 10-7m). The wavelength of light or λ, measured in
nanometers (nm) or Ångstroms (1 nm = 10 Å) is what determines the perceived
color. The frequency of light (f) defines the number of waves occurring
in a given amount of time. Hence, waves become shorter as the frequency
becomes higher, or : λ = c/f, with the speed of light c = 299.705
km/s.
As the color bands blend, their precise lengths vary a little. Hence, their
boundaries are approximate, for the color spectrum is
continuous. Nevertheless, frontiers are present as anyone can see,
although a small measure of arbitrariness cannot be avoided.
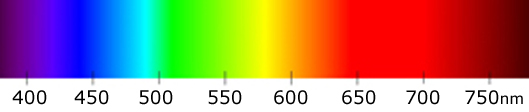
color
spectrum of visible light
Compare the
wavelengths of visible light (defining color), measured in
nanometers, with the
frequencies (defining tone pitch), measured in Hertz. The wavelength bands
given below give rise to a "centre of color gravity" (Newton)
or "color center wavelength", the
mean value of the color band. This wavelength is numerically
compared with the frequencies of the notes at International Pitch
(A4 = 440 Hz) &
Verdi Pitch (A4 = 432 Hz). Their measure of numerical correspondence is then
calculated.
|
TABLE 1 : Defining the Colors of the Notes |
Wavelengths of Visible Spectrum
(in nm) |
Centres of Color Gravity |
Tone Names
Middle C = C4 |
Verdi
Tone Pitches
(in Hz)
A4 = 432Hz |
QBL |
Yoga
Ch'i |
International
Tone Pitches
(in Hz)
A4 = 440Hz |
|
VII VIOLET |
400 to 380 |
390 |
G4 |
384,868 / 5,132
(*)
Δ% = 98,7 (**) |
1 Ur |
7 |
391,995 / 1,995
Δ% = 99,5 |
|
Dark Blue |
420 to 400 |
410 |
G#4
Ab4 |
407,754 / 2,246
Δ% = 99,4 |
2 Ne |
6 |
415,305
/ 5,305
Δ% = 98,7 |
|
VI BLUE |
450 to 420 |
435 |
A4 |
432 / 3
Δ% = 99,3 |
440
/ 5
Δ% = 98,9 |
|
Light Blue |
475 to 450 |
462,5 |
A#4
Bb4 |
457,688 / 4,812
Δ% = 98,96 |
3 Pl |
5 |
466,164
/ 3,664
Δ% = 99,2 |
|
V CYAN |
495 to 475 |
485 |
B4 |
484,904 / 0,096
Δ% = 99,98 |
493,883 / 8,883
Δ% = 98,2 |
|
IV GREEN |
520 to 495 |
507,5 |
C5 |
513,737 / 6,237
Δ% = 39098,8 |
4 Ju
6 Su |
4 |
523,251
/ 15,751
Δ% = 96,99 |
|
Yellow Green |
565 to 520 |
542,5 |
C#5
Db5 |
544,286 / 1,786
Δ% = 99,7 |
5 Ma
8 Me |
3 |
554,365
/ 11,865
Δ% = 97,86 |
|
III YELLOW |
575 to 565 |
570 |
D5 |
576,651 / 6,651
Δ% = 99,5 |
587,33
/ 17,33
Δ% = 97,05 |
|
Yellow Orange |
615 to 575 |
595 |
D#5
Eb5 |
610,94 / 15,940
Δ% = 97,4 |
7 Ve
9 Lu |
2 |
622,254
/ 27,254
Δ% = 95,6 |
|
II ORANGE |
645 to 615 |
630 |
E5 |
647,269 / 17,269
Δ% = 97,3 |
659,255
/ 29,255
Δ% = 95,6 |
|
I RED |
720 to 645 |
682,5 |
F5 |
685,757 / 3,257
Δ% = 99,5 |
10 Sa |
1 |
698,456 / 15,956
Δ% = 97,7 |
|
Dark Red |
750 to 720 |
735 |
F#5
Gb5 |
726,535 / 8,465
Δ% = 98,85 |
739,989 / 4,989
Δ% = 99,3 |
M : 98,95%
σ = 0,17 |
M : 97,9%
σ = 1,33 |
|
(*) numerical difference between Centres of Color
Gravity and Tone Pitch. Examples : for VIOLET (A = 432) : 390 -
384,868 = 5,132 ; for VIOLET (A = 440) : 391,995 - 390 = 1,995 ;
(**) percentual numerical correspondence between
Centres of Color Gravity and Tone
Pitch. Examples : for VIOLET (A = 432) : 100/390 x 384,868 = 98,7% ;
for VIOLET (A = 440) : 100/391,995 x 390 = 99,5%. Counting the times
International Pitch scores better than Verdi Pitch we get 3, whereas
Verdi Pitch is 9 times closer to the heart of the hue. In
International Pitch, C5 falls outside the color interval. On average,
Verdi Pitch is 98,95% corresponding (with a standard deviation of 0,17),
whereas International Pitch is 97,9% corresponding with a much larger
standard deviation (σ = 1,33).
The strength of the linear association between the two variables R (centre
of color gravity & tone pitch with A = 432 Hz or A = 440 Hz) is R = 1, or
strong correlation (Pearson). |

chromatic
scale (starting with G) with color correspondences
"The structure of the true octave is derived
from the overtone series, from which nothing more complete than the
comprehensive building material furnished by the chromatic
twelve-tone scale can be developed." -
Hindemith (1942, Book 1, p.52).
Both scientists & artists have disputed the validity of the
alignment. However, it cannot be denied a proportionality and strong
correlation is at work here. Can this be applied to the harmonic
series ?
§ 5 The Harmonic
Series
In music, the harmonic
series is an acoustical phenomenon defined by a sequence of pitches
related to a lower pitch. This is a sequence of successive intervals
: octave (2:1), fifth (3:2), fourth (4:3), major third (5:4), minor
third (6:5), two intervals between a minor third and a whole tone
(7:6 & 8:7), a large whole tone (9:8), a small whole tone (10:9), a
minor second (16:15) and progressively smaller intervals ad
infinitum. For example : take a long string or tube (1:1), then
the ratio of 3:2 implies a string or a tube of 2/3 length will sound
a fifth higher in pitch than the longer one. At one and a half times
the lenght will sound a fifth lower.
The prevalence of the octave, fifth, fourth, major & minor third in
the lower part of the series contributed to the development of the
concept of harmony. The intervals of the harmonic series are called
"harmonic intervals" and they are all acoustically pure (beatless).
When an instrument plays a single musical tone, a whole frequency spectrum
is generated. It consists of a fundamental
frequency (the 1th harmonic or 1th partial) and all the overtones present
together with the fundamental tone.
A "harmonic" is an
integer (whole number) multiple of the fundamental frequency of a
vibrating object. The noise of a drill also generates a series of
overtones, but these clash and beat each other up. Musical tones
satisfy the conditions of harmony and so the overtones work
together with no beats. The harmonic structure of the overtones
assists in understanding how one tone may move towards another tone
(as in an actual harmonic progression).
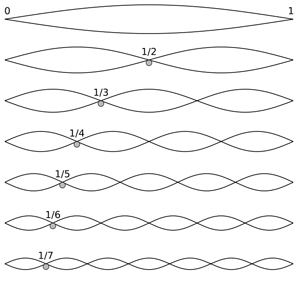
the Harmonic
Series of a string
Suppose this is a string vibrating at 110 Hz. When
it divides itself up in two halves, these vibrate at 220 Hz. Divided
into three thirds, each vibrates at 330 Hz. Divided into four
quaters, each vibrate at 440 Hz. etc. All these vibrations and lots
more happen at the same time, repeating a whole cycle at the lowest,
fundamental frequency involved. Not only do these overtones define
the timbre of tones (primarily by way of the relative
amplitudes of the various harmonics), they are crucial to
understanding the natural harmonic rules of Western tonal
harmony, i.e. a harmonic logic based on the properties of the
harmonic series of every musical note sounded (Hindemith).
The Harmonic Series, defining precise mathematical proportionality, is (together
with the energy or amplitude of the soundwave), the foundation of
every
musical tone. It operates a precise & fixed
mathematical relationship between : 1) all the partials of a tone (the
frequency components of a tone, i.e. fundamental frequency plus
overtones), 2)
the frequency ratio of a tone, 3) the frequency in Hz of a tone and
4) the harmonic interval to the previous tone.
TABLE 2 below has the
16 Harmonics of C, with the corresponding colors for the partials
based on the analysis above (TABLE 1).
|
TABLE 2 : Harmonic Series of C with Color
Correspondences |
|
Partials = 1 Fundamental + 15 Overtones |
Harmonic |
Overtone |
Frequency
Ratio |
Frequency
A4 = 432Hz
C2 = 64,217 Hz |
Tone |
Harmonic
Interval to Previous Tone |
Fundamental
Frequency |
1th |
none |
1:1 |
64,217 |
C2 |
fundamental |
Double
Frequency |
2th |
1th |
2:1 |
128,434 |
C3 |
octave |
Trifold
Frequency |
3th |
2th |
3:2 |
192,651 |
G3 |
fifth |
Fourfold
Frequency |
4th |
3th |
4:3 |
256,868 |
C4 |
fourth |
Fivefold
Frequency |
5th |
4th |
5:4 |
321,085 |
E4 |
major
third |
Sixfold
Frequency |
6th |
5th |
6:5 |
385,302 |
G4 |
minor
third |
Sevenfold
Frequency |
7th |
6th |
7:6 |
449,519 |
Bb4
-31,17c |
|
Eightfold
Frequency |
8th |
7th |
8:7 |
513,737 |
C5 |
Nine
Frequency |
9th |
8th |
9:8 |
577,953 |
D5 |
large
whole tone |
Tenfold
Frequency |
10th |
9th |
10:9 |
642,17 |
E5 |
small
whole tone |
Elevenfold
Frequency |
11th |
10th |
11:10 |
706,387 |
F#5
-48,68c |
|
Twelvefold
Frequency |
12th |
11th |
12:11 |
770,604 |
G5 |
Thirteenfold
Frequency |
13th |
12th |
13:12 |
834,821 |
Ab5
+40,52 |
Fourteenfold
Frequency |
14th |
13th |
14:13 |
899,038 |
Bb5
-31,17 |
Fifteenfold
Frequency |
15th |
14th |
15:14 |
963,255 |
B5 |
Sixteenfold
Frequency |
16th |
15th |
16:15 |
1027,472 |
C6 |
minor
second |
|
The notes in bold have a large offset
(in cents). Bb4, F#5 & Bb5 are lower (-) than indicated, Ab5 is higher
(+).
The frequencies of the overtones are calculated with the fundamental
frequency as their basis (here C2). For example, the 16th Harmonic
has a frequency of 1027,472 Hz or 64,217 Hz x 16. All values in Hz are based on A4 =
432 Hz, or C2 = 64,217 Hz. |
There are two types of
harmonics : odd-numbered (1th, 3th, 5th, 7th & 9th etc.) and
even-numbered (2th, 4th, 6th, 8th, 10th etc.). The presence & power
of these in the frequency spectrum defines the "timbre" of
instruments. In clarinetes, the typical harmonics are the
odd-numbered, whereas in the flutes, even-numbered predominate.
"... the chromatic scale can be derived just as simply from the
overtone series ; that, since it makes exhaustive use the clearest
overtone relations, it has an even more natural basis ; and that it
is thus the most natural of all scales, and the best adapted to
melodic as well as to harmonic use." -
Hindemith (1942, Book 1, p.48).
The higher the harmonic,
the less it is heard. Each octave in the harmonic series is divided
into increasingly "smaller" and more numerous intervals. The first
eight harmonics define the tone and also contain the fundamental
triad (tonic) of the tonic scales erected on it, the gravity of the
tone. The intervals (to
the previous tone) defined by the harmonic series are "pure"
& "just", i.e. in accordance with natural law, i.e. unison
(1/1, frequency ratio : 1:1), octave (2/1, frequency ratio : 2:1),
fifth (3/2, frequency ratio : 3:2), fourth (4/3, frequency ratio :
4:3), major third (5/4, frequency ratio : 5:4) & minor third (6/8,
frequency ratio : 6:5).
The frequency ratios of
the first 6 harmonics (1 - 6) define the acoustico-numerical proportions of 5
important intervals (or distances between two notes). These are the
harmonic intervals or "perfect" consonances. The first 4
harmonics (first three overtones) define harmonic octave (= 2:1, C - C),
harmonic fifth (= 3:2, C - G) & harmonic fourth
(= 4:3, G - C). The intervals of a harmonic fifth & a harmonic
fourth make an octave (3:2 + 4:3 = 12/6 = 2:1) The harmonic fifth &
the harmonic fourth are relatively beatless. As the 3th
harmonic has an offset of +2c, they do have a beat, but one
imperceptible to the human ear (able to distinguish a difference of
5 to 6c). Only the harmonic octave is absolutely beatless.
This is why the 1th harmonic is the fundamental frequency of the
tone, the backbone of the harmonic series in question. Pure, perfect
intervals like harmonic octave, harmonic fourth & harmonic fifth are
intervals with zero beat or a beat below 5c. Harmonic octave &
harmonic fifth are consonant intervals. Depending of context, the
harmonic fourth can be dissonant or consonant (in fact, C - F, the
fourth from the root) is not part of the harmonic series
(instead F# is the 10th overtone, but with an offset of -48,68c) !
In the Harmonic Series, the fundamental with 2 overtones (1th, 2th &
3th harmonic) is followed by the harmonic major third (= 5:4, C - E) and the
harmonic minor
third (= 6:5, E - G). The harmonic third has two forms : major &
minor. The difference in
size between these two harmonic thirds is a harmonic minor second.
The harmonic thirds too are
beatless. The intervals of a major & minor harmonic sixth do not
occur between adjacent partials. To identify them, we need to
leap. The harmonic major sixth has frequency ratio 5:3, the harmonic
minor sixth 8:5. Because of their mixed formats (major versus
minor), these 4 intervals are all "imperfect" consonances.
The frequencies of the Harmonic Series, being integer multiples of
the fundamental frequency, are naturally (bio-acoustically)
related to each other by whole-numbered & small whole-numbered
ratios. This is the basis of the consonance of musical intervals.
The Harmonic Series diverges in a way like the Fibonacci sequence does and
can be rearranged with limit points integrating the Golden Ratio
(φ). The auditive (bio-acoustic) & psycho-acoustic impact of forcing
the ear to adjust to a non-φ based Master Tuning (like A4 = 440 Hz)
is therefore questionable. The objective, natural form of the Harmonic
Series (comparable to φ) is best assisted by a standard frequency
based on φ, thereby stimulating an ear constructed by way of φ. In this way,
source, medium & receiver are co-relatively attuned.
|
TABLE 3 : Harmonic Series of the Notes of the
Chromatic Scale with their Colors (A4 = 432 Hz) |
|
Note |
02th |
03th |
04th |
05th |
06th |
07th |
08th |
09th |
10th |
11th |
12th |
13th |
14th |
15th |
16th |
|
f (Hz) |
| C2 |
C3 |
G3 |
C4 |
E4 |
G4 |
Bb4
(-) |
C5 |
D5 |
E5 |
F#5
(-) |
G5 |
Ab5
(+) |
Bb5
(-) |
B5 |
C6 |
|
64,217 |
| C#2 |
C#3 |
G#3 |
C#4 |
F4 |
G#4 |
B4
(-) |
C#5 |
D#5 |
F5 |
G5
(-) |
G#5 |
A5
(+) |
B5
(-) |
C6 |
C#6 |
| 68,036 |
| D2 |
D3 |
A3 |
D4 |
F#4 |
A4 |
C5
(-) |
D5 |
E5 |
F#5 |
G#5
(-) |
A5 |
A#5
(+) |
C6
(-) |
C#6 |
D6 |
| 72,081 |
| D#2 |
D#3 |
A#3 |
D#4 |
G4 |
A#4 |
C#5
(-) |
D#5 |
F5 |
G5 |
A5
(-) |
A#5 |
B5
(+) |
C#6
(-) |
D6 |
D#6 |
| 76,368 |
| E2 |
E3 |
B3 |
E4 |
G#4 |
B4 |
D5
(-) |
E5 |
F#5 |
G#5 |
A#5
(-) |
B5 |
C6
(+) |
D6
(-) |
D#6 |
E6 |
| 80,909 |
| F2 |
F3 |
C4 |
F4 |
A4 |
C5 |
D#5
(-) |
F5 |
G5 |
A5 |
B5
(-) |
C6 |
C#6
(+) |
D#6
(-) |
E6 |
F6 |
| 85,72 |
| F#2 |
F#3 |
C#4 |
F#4 |
A#4 |
C#5 |
E5
(-) |
F#5 |
G#5 |
A#5 |
C6
(-) |
C#6 |
D6
(+) |
E6
(-) |
F6 |
F#6 |
| 90,817 |
|
G2 |
G3 |
D4 |
G4 |
B4 |
D5 |
F5
(-) |
G5 |
A5 |
B5 |
C#6
(-) |
D6 |
D#6
(+) |
F6
(-) |
F#6 |
G6 |
| 96,217 |
|
G#2 |
G#3 |
D#4 |
G#4 |
C5 |
D#5 |
F#5
(-) |
G#5 |
A#5 |
C6 |
D6
(-) |
D#6 |
E6
(+) |
F#6
(-) |
G6 |
G#6 |
|
101,938 |
|
A2 |
A3 |
E4 |
A4 |
C#5 |
E5 |
G5
(-) |
A5 |
B5 |
C#6 |
D#6
(-) |
E6 |
F6
(+) |
G6
(-) |
G#6 |
A6 |
| 108 |
| A#2 |
A#3 |
F4 |
A#4 |
D5 |
F5 |
G#5
(-) |
A#5 |
C6 |
D6 |
E6
(-) |
F6 |
F#6
(+) |
G#6
(-) |
A6 |
A#6 |
| 114,422 |
| B2 |
B3 |
F#4 |
B4 |
D#5 |
F#5 |
A5
(-) |
B5 |
C#6 |
D#6 |
F6
(-) |
F#6 |
G6
(+) |
A6
(-) |
A#6 |
B6 |
| 121,226 |
| The
fundamental frequency of the notes are based on A4 = 432 Hz or
A2 = 108 Hz. The frequencies of the first sixteen harmonics can
be calculated by multiplying the fundamental frequency with the
corresponding numerator of the frequency ratio of the harmonic
in question (cf. Table 2). For example : F2 (f = 85,72 Hz), so
the 15th Harmonics = f.15 = 85,72 x 15 = 1285,8 Hz. The
notes with a large offset (+/- 30 cents) are always the 7th,
11th, 13th & 14th harmonics, with "+" ("-") indicating they are
higher (lower) than indicated. |
Harmonic unison,
harmonic octave, harmonic second, major & minor harmonic third,
harmonic fourth, harmonic fifth, major & minor harmonic sixth are consonant.
The harmonic series also contains the harmonic minor second (16:15)
and the harmonic minor seventh or "septimal minor seventh" (7:4).
The latter is also an interval not occuring between adjacent
partials. Together (at times) with the harmonic fourth, the minor harmonic
second and the minor harmonic seventh are dissonant.
The 10 harmonic intervals at work in the harmonic series of every
musical tone are the basis of what could be called a "natural" tonal
harmony. However, for all kinds of reasons, musical practice
deviates from this natural harmonic law, introducing a cultural
harmonic practice and reinforcing it. This is fine as long as the
deviation does not cause the sound to become too harsh and
unmusical, hampering the experience of beauty. So although in music
culture may & does alter nature, there is a limit to this. But this
remains to a certain degree (inter)subjective.
§ 6 Defining Tonal
Scales

Blind
Harpist with Harp tuned to a Heptatonic Scale ?
Relief in Tomb Chapel of Paatonemheb (ca. 1333-1319 BCE)
Noise is a sound with an irregular, amorph frequency spectrum.
A musical tone (note) is a sound defined by the Harmonic Series and its integer
frequency patterns. Besides defining timbre or the "instrument
color" of a tone when sounded, the Harmonic Series refers to six
important frequency
ratio's : 1/1, 2/1, 3/2, 4/3, 5/4, 6/5 (or the harmonic intervals of
unison, octave, fifth, fourth, major third & minor third to the previous
note). These play a fundamental role in the elaboration of the
system of 24 tonic scales defining classical (tonal) harmony. This
direct relationship between tonal harmony and the Harmonic Series is
often overlooked.
|
TABLE 4 : Harmonic Intervals |
|
consonant |
dissonant |
| perfect |
imperfect |
(minor) second, fourtht+1
(minor) seventh |
|
unison, fourtht, fifth, octave |
major & minor
thirds & sixths |
When two strings are
tuned an absolutely beatless interval like the octave apart, the question of
how to divide the octave gives rise to scales.
A scale is an organized, attuned and characterisic "family of tones",
all being frequency-wise relatives.
Historically, the first scale to be formed was the pentatonic scale.
To play on a six stringed harp, a pentatonic scale can be generated
consisting of the fundamental tone (C), the octave of this tone (C)
and four other notes (G, D & A). This scale of five steps : C, D, E, G, A, C
(the first pentatonic mode), and all other pentatonic scales consist of
tones having related frequencies with few beats. The members
of each clan, family or team naturally co-operate because they
continuously gravitate around each other, forming enduring dependent
originations, the "solid" architectures of conventional reality.
The pentatonic group of scales (set of families) was adopted
by just about every human society.
The pentatonic scales can be derived by the simple proportions given
by five consecutive pitches from the circle of fifths : C, G,
D, A and E. The ability to tune a harp to the pentatonic scale is
the cornerstone of the development of music.
While all notes on this scale sound "in tune" together (no major
discord can be gotten), they do not define any stong "harmonic
pull", i.e. the clear tendency of tonet to ask for
tonet+1. The latter is the functional reciprocity of a
tone in terms of the type or "color" of the family of tones to which
it belongs. The pentatonic scales lack semitones. Therefore,
every
single combinates sounds euphonious. This also explains the
staticity of pentatonic music. There is no real sense of
harmonic transition or progression to be construed on the basis of the selected
five tones.
The circles of fifths, giving rise to the pentatonic scales, produce
five pentatonic modes. The first pentatonic mode, with C as its
first note or "tonic", is defined by whole note (T or two semitones)
& a minor third (M or three semitones) : TTMTM. This
minor interval of
three semitones is the special feature of all pentatonic scales,
giving this group a self-contained harmonic acoustic identity.
|
TABLE 5 : The Pentatonic Modes |
|
Circle of Fifths |
Scale |
Pentatonic Mode |
Transposition
Rule |
Steps |
| C |
C, D, E, G, A, C |
I |
TTMTM |
2-2-3-2-3 |
| G |
G, A, C, D, E, G |
II |
TMTTM |
2-3-2-2-3 |
| D |
D, E, G, A, C, D |
III |
TMTMT |
2-3-2-3-2 |
| A |
A, C, D, E, G, A |
IV |
MTTMT |
3-2-2-3-2 |
| E |
E, G, A, C, D, E |
V |
MTMTT |
3-2-3-2-2 |
The relative absence of
harmonic push-and-pull dynamism (voice leading or harmonic
progression) in the pentatonic system, gave
rise to further subdivisions of the octave, introducing two new
intervals (from C as first tone) : the fourth (F) & seventh (B), together
dividing the octave in seven steps (for C) : C, D, E, F, G, A & B ;
the heptatonic scale.
This scale, with C as its first tone or
"tonic", is defined by 5 whole tones (T = two semitones) & 2
semitones (S = one semitone) : TTSTTTS. This can be done for each
tone of the scale, bringing forth seven scales. These were called "modes" and given the names
of the 7 provinces of Ancient Greece :
|
TABLE 6 : The Greek (or Ecclesiastical) Modes |
|
Tonic |
Scale |
Mode |
Transposition Rule |
Steps |
| C |
C, D, E, F, G,
A, B, C |
Ionian |
TTSTTTS |
2-2-1-2-2-2-1 |
| D |
D, E, F, G, A, B, C, D |
Dorian |
TSTTTST |
2-1-2-2-2-1-2 |
| E |
E, F, G, A, B, C, D, E |
Phyrgian |
STTTSTT |
1-2-2-2-1-2-2 |
| F |
F, G, A, B, C, D, E, F |
Lydian |
TTTSTTS |
2-2-2-1-2-2-1 |
| G |
G, A, B, C, D, E, F, G |
Mixolydian |
TTSTTST |
2-2-1-2-2-1-2 |
| A |
A, B, C, D, E, F, G, A |
Aeolian |
TSTTSTT |
2-1-2-2-1-2-2 |
| B |
B, C, D, E, F, G, A, B |
Locrian |
STTSTTT |
1-2-2-1-2-2-2 |
The Greek modes were
used in the Middle Ages and associated with spirito-acoustic
properties. They continued to be used in Late Hellenism and the
Middle Ages. In the Renaissance (starting in painting as early as
the 13th century), individuality, coloration and
stronger expressiveness begin to bloom, giving rise (in Modern
Times), to the idea of specific "key colors", each family of tones
expressing an overall timbre linked with musical ideas. The
difference between a major & minor third, defined by a semitone, played a
crucial role in this. Shades of loud beats ("major") and shades of
softer beats ("minor") could be generated. The scales themselves had
characteristic content & dynamic push-and-pull behaviors.
Of the seven Greek Modes, only two were deemed to satisfy the
conditions of well-organized harmonies able to express the "major" /
"minor" contrast in the form of closely related families of seven
notes. The Ionian mode, with its very obvious "full
stops" at the end of every "harmonic sentence" (or combinations of
simultaneously sounding notes), obviously became the foundation for
the scales integrating the extraverted major third, while the
Aeolian mode, with less obvious definite full stops, set the
standard for the scales based on the introverted minor third.
The Ionian pattern of TTSTTTS
was applied to every note of the chromatic scale. This yields 12
so-called "major" scales. The first scale of this series is C major
(C, D, E, F, G, A, B, C).
The Aeolian pattern of
TSTTSTT applied to the chromatic scale generates 12
so-called "minor" scales. The
first scale of this series is a minor (A, B, C, D, E, F, G, A). On
each of the seven steps (or degrees from I to VII) of the major
scales, triads could be formed.
In the major scales, the major triads are on I, IV & V, the minor
triads on II, III & VI and the diminished triad on VII (the third &
fifth are lowered with a semitone). In the (natural) minor scales,
the minor triads are on I & IV, the major triad on V & VI , the
diminished triads on II & VII, and the augmented triad on III (the
fifth is raised with a semitone).
The
scales directly generated by the Aeolian mode were also
called "antique" or "natural". Because these always end with an
interval of a whole tone at the end (g - a in a minor), a clearer
"lead tone" (one naturally moving towards the tonic) was introduced
by raising the last step (g in a minor) with a semitone (to g# in a
minor). This generated the harmonic minor scales. As this
first adjustment
brings about an augmented interval (f - g# in a minor), f was also
raised to f# (in a minor). An augmented interval was
preferably avoided in older music and is even hard to sing in tune
today. This second adjustment generated the melodic minor scales. The change
from f to f# (in a minor), i.e. the transformation of the antique
minor to the melodic minor only occurs when the melody moves
upwards. In a downward movement, f# is restored to f and the
descending melodic minor returns (equals) the antique minor.
This set of 24 scales defines the foundation of the classical, tonal
harmony of Western music.
The fundamental issue with the tonal system is the balance between
the natural Harmonic Series and the degree of tempering of the natural
(just, harmonic) intervals. This refers to the Tuning System,
another crucial factor often overlooked in contemporary manuals on
harmony. No doubt because the matter is (at first sigh) too complex
and calls for a "harmonic diplomacy" difficult to teach. Indeed, the
Tuning System involves
"... a compromise between the natural
intervals and our inability to use them - that compromise we call
the tempered system, which amounts to an indefinitely extended
truce." -
Schoenberg
(1983, p.25.)
§ 7 The Tuning System
While frequency in Hertz
(the nominal lower frequency limit of human hearing being 20 Hz with
a capacity to differentiate between two tones 1 to 2 Hz apart)
gives the precise "location" of the tones, to further define
scales, especially in terms of their tuning system, we need a
unit to measure the distance (intervals) between these located
tones, i.e. their frequency ratios. This unit is "cent" (c) or
"one hundred", introduced by Alexander Ellis in 1875. This a
logaritmic scale with 1200c to the octave. Given frequency ratio
a:b, we get the following : cent = (log2 a:b) x 1200, or,
given the fifth (3:2) we get : log2 3:2 = log2
(1,5) = 0,584963 x 1200 = 701,956c. Cents are used to express the
size of the microintervals (intervals smaller than one whole tone).
The fundamental question is : does the tuning system follow the
acoustical laws of audition, objectively (Harmonic Series) and
subjectively (structure & function of the human ear) ? Simply put,
does tuning follow natural acoustic law ? Technically, this is the number of pure,
harmonic intervals present in the scale. Equal Temperament has the least pure
intervals present (namely one, the octave). But the octave merely
delimits the scale, and does not functionally contribute to the
division of the octave. So Equal Temperament is the less natural
scalar definition.
The harmonic intervals are the reference of all acoustically based tuning
systems, for these are beatless intervals, i.e. acoustically pure
and mathematically simple (integers instead of real numbers).
They are also called "just intervals". Scalar definitions based on them are
untempered.
|
TABLE 7 : Ratios & Cents of Core Harmonic Intervals |
|
Interval |
Frequency Ratio |
Cents |
|
unison |
1:1 |
0 |
|
octave |
2:1 |
1200 |
|
fifth |
3:2 |
701,956 |
|
fourth |
4:3 |
498,044 |
|
major third |
5:4 |
386,314 |
|
minor third |
6:5 |
315,641 |
When the intervals are expressed as cents, the differences between
the intervals of different tuning systems can be easily compared. In Equal
Temperament, the standard tuning system, the intervals are always
multiples of one hundred. This equalization of the microintervals is
the cause of the "grayness" of this tuning system, eliminating the
specific "key colors" of the tonal scales (eliminating the
difference between the chromatic & the diatonic semitone, defining
the semitone as 50c, tempering all octave-dividing intervals). Its main advantage is
tuning facility (especially on keyboards) and standardization.
Equal Temperament, commonly
used everywhere today, has been rightly accused to
"ruin harmony" (Duffin,
2007).
|
TABLE 8 : Equal Temperament |
|
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
C |
|
000c |
100c |
200c |
300c |
400c |
500c |
600c |
700c |
800c |
900c |
1000c |
1100c |
1200c |
There is no direct
relationship between Hz and c. The former positions absolute
frequency, the latter proportional position (or interval distance between
tones). We need to know the standard tuning (or Master Tuning) to
relate both values. Indeed, as a tone increases in pitch, its
location changes and so also its distance from other static tones.
But the Hz value and the cent value are not measured one-to-one,
since often one value increases while the other decreases.
|
TABLE 9 : Frequency (Hz) /
cents relationships
for A4 = 432 Hz (C3 = 128,434 Hz = 0c) |
|
Cents |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
|
-50 |
124,778 |
132,198 |
140,059 |
148,387 |
157,211 |
166,559 |
176,463 |
186,956 |
198,073 |
209,851 |
222,329 |
235,550 |
|
-49 |
124,850 |
132,274 |
140,140 |
148,473 |
157,301 |
166,655 |
176,565 |
187,064 |
198,187 |
209,972 |
222,458 |
235,686 |
|
-48 |
124,922 |
132,351 |
140,221 |
148,559 |
157,392 |
166,751 |
176,667 |
187,172 |
198,302 |
210,093 |
222,586 |
235,822 |
|
-47 |
124,995 |
132,427 |
140,302 |
148,644 |
157,483 |
166,848 |
176,769 |
187,280 |
198,416 |
210,215 |
222,715 |
235,958 |
|
-46 |
125,067 |
132,504 |
140,383 |
148,730 |
157,574 |
166,944 |
176,871 |
187,388 |
198,531 |
210,336 |
222,844 |
236,095 |
|
-45 |
125,139 |
132,580 |
140,464 |
148,816 |
157,665 |
167,041 |
176,973 |
187,497 |
198,646 |
210,458 |
222,972 |
236,231 |
|
-44 |
125,211 |
132,657 |
140,545 |
148,902 |
157,756 |
167,137 |
177,076 |
187,605 |
198,761 |
210,579 |
223,101 |
236,367 |
|
-43 |
125,284 |
132,733 |
140,626 |
148,988 |
157,847 |
167,234 |
177,178 |
187,713 |
198,875 |
210,701 |
223,230 |
236,504 |
|
-42 |
125,356 |
132,810 |
140,707 |
149,074 |
157,939 |
167,330 |
177,280 |
187,822 |
198,990 |
210,823 |
223,359 |
236,641 |
|
-41 |
125,428 |
132,887 |
140,789 |
149,160 |
158,030 |
167,427 |
177,383 |
187,930 |
199,105 |
210,945 |
223,488 |
236,777 |
|
Cents |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
|
-40 |
125,501 |
132,964 |
140,870 |
149,247 |
158,121 |
167,524 |
177,485 |
188,039 |
199,220 |
211,067 |
223,617 |
236,914 |
|
-39 |
125,573 |
133,040 |
140,951 |
149,333 |
158,213 |
167,620 |
177,588 |
188,148 |
199,335 |
211,189 |
223,746 |
237,051 |
|
-38 |
125,646 |
133,117 |
141,033 |
149,419 |
158,304 |
167,717 |
177,690 |
188,256 |
199,451 |
211,311 |
223,876 |
237,188 |
|
-37 |
125,719 |
133,194 |
141,114 |
149,505 |
158,395 |
167,814 |
177,793 |
188,365 |
199,566 |
211,433 |
224,005 |
237,325 |
|
-36 |
125,791 |
133,271 |
141,196 |
149,592 |
158,487 |
167,911 |
177,896 |
188,474 |
199,681 |
211,555 |
224,134 |
237,462 |
|
-35 |
125,864 |
133,348 |
141,277 |
149,678 |
158,579 |
168,008 |
177,998 |
188,583 |
199,797 |
211,677 |
224,264 |
237,599 |
|
-34 |
125,937 |
133,425 |
141,359 |
149,765 |
158,670 |
168,105 |
178,101 |
188,692 |
199,912 |
211,799 |
224,394 |
237,737 |
|
-33 |
126,009 |
133,502 |
141,441 |
149,851 |
158,762 |
168,202 |
178,204 |
188,801 |
200,027 |
211,922 |
224,523 |
237,874 |
|
-32 |
126,082 |
133,579 |
141,522 |
149,938 |
158,854 |
168,300 |
178,307 |
188,910 |
200,143 |
212,044 |
224,653 |
238,012 |
|
-31 |
126,155 |
133,657 |
141,604 |
150,024 |
158,945 |
168,397 |
178,410 |
189,019 |
200,259 |
212,167 |
224,783 |
238,149 |
|
Cents |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
|
-30 |
126,228 |
133,734 |
141,686 |
150,111 |
159,037 |
168,494 |
178,513 |
189,128 |
200,374 |
212,289 |
224,913 |
238,287 |
|
-29 |
126,301 |
133,811 |
141,768 |
150,198 |
159,129 |
168,591 |
178,616 |
189,237 |
200,490 |
212,412 |
225,043 |
238,424 |
|
-28 |
126,374 |
133,888 |
141,850 |
150,285 |
159,221 |
168,689 |
178,720 |
189,347 |
200,606 |
212,535 |
225,173 |
238,562 |
|
-27 |
126,447 |
133,966 |
141,932 |
150,372 |
159,313 |
168,786 |
178,823 |
189,456 |
200,722 |
212,657 |
225,303 |
238,700 |
|
-26 |
126,520 |
134,043 |
142,014 |
150,458 |
159,405 |
168,884 |
178,926 |
189,566 |
200,838 |
212,780 |
225,433 |
238,838 |
|
-25 |
126,593 |
134,121 |
142,096 |
150,545 |
159,497 |
168,981 |
179,030 |
189,675 |
200,954 |
212,903 |
225,563 |
238,976 |
|
-24 |
126,666 |
134,198 |
142,178 |
150,632 |
159,589 |
169,079 |
179,133 |
189,785 |
201,070 |
213,026 |
225,693 |
239,114 |
|
-23 |
126,739 |
134,276 |
142,260 |
150,719 |
159,682 |
169,177 |
179,237 |
189,894 |
201,186 |
213,149 |
225,824 |
239,252 |
|
-22 |
126,813 |
134,353 |
142,342 |
150,806 |
159,774 |
169,274 |
179,340 |
190,004 |
201,302 |
213,273 |
225,954 |
239,390 |
|
-21 |
126,886 |
134,431 |
142,425 |
150,894 |
159,866 |
169,372 |
179,444 |
190,114 |
201,419 |
213,396 |
226,085 |
239,529 |
|
Cents |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
|
-20 |
126,959 |
134,509 |
142,507 |
150,981 |
159,959 |
169,470 |
179,547 |
190,224 |
201,535 |
213,519 |
226,216 |
239,667 |
|
-19 |
127,033 |
134,586 |
142,589 |
151,068 |
160,051 |
169,568 |
179,651 |
190,334 |
201,652 |
213,642 |
226,346 |
239,805 |
|
-18 |
127,106 |
134,664 |
142,672 |
151,155 |
160,143 |
169,666 |
179,755 |
190,444 |
201,768 |
213,766 |
226,477 |
239,944 |
|
-17 |
127,179 |
134,742 |
142,754 |
151,243 |
160,236 |
169,764 |
179,859 |
190,554 |
201,885 |
213,889 |
226,608 |
240,083 |
|
-16 |
127,253 |
134,820 |
142,836 |
151,330 |
160,329 |
169,862 |
179,963 |
190,664 |
202,001 |
214,013 |
226,739 |
240,221 |
|
-15 |
127,326 |
134,898 |
142,919 |
151,417 |
160,421 |
169,960 |
180,067 |
190,774 |
202,118 |
214,137 |
226,870 |
240,360 |
|
-14 |
127,400 |
134,976 |
143,002 |
151,505 |
160,514 |
170,059 |
180,171 |
190,884 |
202,235 |
214,260 |
227,001 |
240,499 |
|
-13 |
127,474 |
135,054 |
143,084 |
151,592 |
160,607 |
170,157 |
180,275 |
190,995 |
202,352 |
214,384 |
227,132 |
240,638 |
|
-12 |
127,547 |
135,132 |
143,167 |
151,680 |
160,699 |
170,255 |
180,379 |
191,105 |
202,469 |
214,508 |
227,263 |
240,777 |
|
-11 |
127,621 |
135,210 |
143,250 |
151,768 |
160,792 |
170,353 |
180,483 |
191,215 |
202,586 |
214,632 |
227,395 |
240,916 |
|
Cents |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
|
-10 |
127,695 |
135,288 |
143,332 |
151,855 |
160,885 |
170,452 |
180,587 |
191,326 |
202,703 |
214,756 |
227,526 |
241,055 |
|
-9 |
127,768 |
135,366 |
143,415 |
151,943 |
160,978 |
170,550 |
180,692 |
191,436 |
202,820 |
214,880 |
227,657 |
241,195 |
|
-8 |
127,842 |
135,444 |
143,498 |
152,031 |
161,071 |
170,649 |
180,796 |
191,547 |
202,937 |
215,004 |
227,789 |
241,334 |
|
-7 |
127,916 |
135,522 |
143,581 |
152,119 |
161,164 |
170,748 |
180,901 |
191,658 |
203,054 |
215,128 |
227,921 |
241,473 |
|
-6 |
127,990 |
135,601 |
143,664 |
152,207 |
161,257 |
170,846 |
181,005 |
191,768 |
203,171 |
215,253 |
228,052 |
241,613 |
|
-5 |
128,064 |
135,679 |
143,747 |
152,295 |
161,350 |
170,945 |
181,110 |
191,879 |
203,289 |
215,377 |
228,184 |
241,753 |
|
-4 |
128,138 |
135,757 |
143,830 |
152,383 |
161,444 |
171,044 |
181,214 |
191,990 |
203,406 |
215,502 |
228,316 |
241,892 |
|
-3 |
128,212 |
135,836 |
143,913 |
152,471 |
161,537 |
171,142 |
181,319 |
192,101 |
203,524 |
215,626 |
228,448 |
242,032 |
|
-2 |
128,286 |
135,914 |
143,996 |
152,559 |
161,630 |
171,241 |
181,424 |
192,212 |
203,641 |
215,751 |
228,580 |
242,172 |
|
-1 |
128,360 |
135,993 |
144,079 |
152,647 |
161,724 |
171,340 |
181,529 |
192,323 |
203,759 |
215,875 |
228,712 |
242,312 |
|
Cents |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
|
0 |
128,434 |
136,071 |
144,163 |
152,735 |
161,817 |
171,439 |
181,634 |
192,434 |
203,877 |
216,000 |
228,844 |
242,452 |
|
1 |
128,509 |
136,150 |
144,246 |
152,823 |
161,911 |
171,538 |
181,739 |
192,545 |
203,995 |
216,125 |
228,976 |
242,592 |
|
2 |
128,583 |
136,229 |
144,329 |
152,912 |
162,004 |
171,637 |
181,844 |
192,657 |
204,113 |
216,250 |
229,109 |
242,732 |
|
3 |
128,657 |
136,307 |
144,413 |
153,000 |
162,098 |
171,737 |
181,949 |
192,768 |
204,230 |
216,375 |
229,241 |
242,872 |
|
4 |
128,731 |
136,386 |
144,496 |
153,088 |
162,191 |
171,836 |
182,054 |
192,879 |
204,348 |
216,500 |
229,373 |
243,013 |
|
5 |
128,806 |
136,465 |
144,580 |
153,177 |
162,285 |
171,935 |
182,159 |
192,991 |
204,467 |
216,625 |
229,506 |
243,153 |
|
6 |
128,880 |
136,544 |
144,663 |
153,265 |
162,379 |
172,035 |
182,264 |
193,102 |
204,585 |
216,750 |
229,639 |
243,294 |
|
7 |
128,955 |
136,623 |
144,747 |
153,354 |
162,473 |
172,134 |
182,370 |
193,214 |
204,703 |
216,875 |
229,771 |
243,434 |
|
8 |
129,029 |
136,702 |
144,830 |
153,442 |
162,567 |
172,233 |
182,475 |
193,325 |
204,821 |
217,000 |
229,904 |
243,575 |
|
9 |
129,104 |
136,781 |
144,914 |
153,531 |
162,661 |
172,333 |
182,580 |
193,437 |
204,939 |
217,126 |
230,037 |
243,715 |
|
Cents |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
|
10 |
129,178 |
136,860 |
144,998 |
153,620 |
162,755 |
172,432 |
182,686 |
193,549 |
205,058 |
217,251 |
230,170 |
243,856 |
|
11 |
129,253 |
136,939 |
145,082 |
153,709 |
162,849 |
172,532 |
182,791 |
193,661 |
205,176 |
217,377 |
230,303 |
243,997 |
|
12 |
129,328 |
137,018 |
145,165 |
153,797 |
162,943 |
172,632 |
182,897 |
193,773 |
205,295 |
217,502 |
230,436 |
244,138 |
|
13 |
129,402 |
137,097 |
145,249 |
153,886 |
163,037 |
172,732 |
183,003 |
193,885 |
205,414 |
217,628 |
230,569 |
244,279 |
|
14 |
129,477 |
137,176 |
145,333 |
153,975 |
163,131 |
172,831 |
183,108 |
193,997 |
205,532 |
217,754 |
230,702 |
244,420 |
|
15 |
129,552 |
137,256 |
145,417 |
154,064 |
163,225 |
172,931 |
183,214 |
194,109 |
205,651 |
217,880 |
230,835 |
244,562 |
|
16 |
129,627 |
137,335 |
145,501 |
154,153 |
163,320 |
173,031 |
183,320 |
194,221 |
205,770 |
218,006 |
230,969 |
244,703 |
|
17 |
129,702 |
137,414 |
145,585 |
154,242 |
163,414 |
173,131 |
183,426 |
194,333 |
205,889 |
218,131 |
231,102 |
244,844 |
|
18 |
129,777 |
137,494 |
145,669 |
154,331 |
163,508 |
173,231 |
183,532 |
194,445 |
206,008 |
218,258 |
231,236 |
244,986 |
|
19 |
129,852 |
137,573 |
145,754 |
154,421 |
163,603 |
173,331 |
183,638 |
194,558 |
206,127 |
218,384 |
231,369 |
245,127 |
|
Cents |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
|
20 |
129,927 |
137,653 |
145,838 |
154,510 |
163,697 |
173,431 |
183,744 |
194,670 |
206,246 |
218,510 |
231,503 |
245,269 |
|
21 |
130,002 |
137,732 |
145,922 |
154,599 |
163,792 |
173,532 |
183,850 |
194,783 |
206,365 |
218,636 |
231,637 |
245,411 |
|
22 |
130,077 |
137,812 |
146,006 |
154,688 |
163,887 |
173,632 |
183,956 |
194,895 |
206,484 |
218,762 |
231,771 |
245,552 |
|
23 |
130,152 |
137,891 |
146,091 |
154,778 |
163,981 |
173,732 |
184,063 |
195,008 |
206,603 |
218,889 |
231,905 |
245,694 |
|
24 |
130,227 |
137,971 |
146,175 |
154,867 |
164,076 |
173,833 |
184,169 |
195,120 |
206,723 |
219,015 |
232,039 |
245,836 |
|
25 |
130,302 |
138,051 |
146,260 |
154,957 |
164,171 |
173,933 |
184,276 |
195,233 |
206,842 |
219,142 |
232,173 |
245,978 |
|
26 |
130,378 |
138,130 |
146,344 |
155,046 |
164,266 |
174,033 |
184,382 |
195,346 |
206,962 |
219,268 |
232,307 |
246,120 |
|
27 |
130,453 |
138,210 |
146,429 |
155,136 |
164,361 |
174,134 |
184,489 |
195,459 |
207,081 |
219,395 |
232,441 |
246,263 |
|
28 |
130,528 |
138,290 |
146,513 |
155,225 |
164,456 |
174,235 |
184,595 |
195,572 |
207,201 |
219,522 |
232,575 |
246,405 |
|
29 |
130,604 |
138,370 |
146,598 |
155,315 |
164,551 |
174,335 |
184,702 |
195,685 |
207,321 |
219,649 |
232,710 |
246,547 |
|
Cents |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
|
30 |
130,679 |
138,450 |
146,683 |
155,405 |
164,646 |
174,436 |
184,809 |
195,798 |
207,441 |
219,776 |
232,844 |
246,690 |
|
31 |
130,755 |
138,530 |
146,767 |
155,495 |
164,741 |
174,537 |
184,915 |
195,911 |
207,560 |
219,903 |
232,979 |
246,832 |
|
32 |
130,830 |
138,610 |
146,852 |
155,584 |
164,836 |
174,638 |
185,022 |
196,024 |
207,680 |
220,030 |
233,113 |
246,975 |
|
33 |
130,906 |
138,690 |
146,937 |
155,674 |
164,931 |
174,739 |
185,129 |
196,137 |
207,800 |
220,157 |
233,248 |
247,118 |
|
34 |
130,982 |
138,770 |
147,022 |
155,764 |
165,027 |
174,840 |
185,236 |
196,251 |
207,920 |
220,284 |
233,383 |
247,260 |
|
35 |
131,057 |
138,850 |
147,107 |
155,854 |
165,122 |
174,941 |
185,343 |
196,364 |
208,041 |
220,411 |
233,518 |
247,403 |
|
36 |
131,133 |
138,931 |
147,192 |
155,944 |
165,217 |
175,042 |
185,450 |
196,478 |
208,161 |
220,539 |
233,653 |
247,546 |
|
37 |
131,209 |
139,011 |
147,277 |
156,034 |
165,313 |
175,143 |
185,557 |
196,591 |
208,281 |
220,666 |
233,788 |
247,689 |
|
38 |
131,285 |
139,091 |
147,362 |
156,125 |
165,408 |
175,244 |
185,664 |
196,705 |
208,401 |
220,794 |
233,923 |
247,832 |
|
39 |
131,360 |
139,172 |
147,447 |
156,215 |
165,504 |
175,345 |
185,772 |
196,818 |
208,522 |
220,921 |
234,058 |
247,976 |
|
Cents |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
|
40 |
131,436 |
139,252 |
147,532 |
156,305 |
165,599 |
175,447 |
185,879 |
196,932 |
208,642 |
221,049 |
234,193 |
248,119 |
|
41 |
131,512 |
139,332 |
147,618 |
156,395 |
165,695 |
175,548 |
185,987 |
197,046 |
208,763 |
221,176 |
234,328 |
248,262 |
|
42 |
131,588 |
139,413 |
147,703 |
156,486 |
165,791 |
175,649 |
186,094 |
197,160 |
208,883 |
221,304 |
234,464 |
248,406 |
|
43 |
131,664 |
139,494 |
147,788 |
156,576 |
165,887 |
175,751 |
186,201 |
197,274 |
209,004 |
221,432 |
234,599 |
248,549 |
|
44 |
131,740 |
139,574 |
147,874 |
156,667 |
165,983 |
175,852 |
186,309 |
197,388 |
209,125 |
221,560 |
234,735 |
248,693 |
|
45 |
131,817 |
139,655 |
147,959 |
156,757 |
166,078 |
175,954 |
186,417 |
197,502 |
209,246 |
221,688 |
234,870 |
248,836 |
|
46 |
131,893 |
139,735 |
148,045 |
156,848 |
166,174 |
176,056 |
186,524 |
197,616 |
209,367 |
221,816 |
235,006 |
248,980 |
|
47 |
131,969 |
139,816 |
148,130 |
156,938 |
166,270 |
176,157 |
186,632 |
197,730 |
209,488 |
221,944 |
235,142 |
249,124 |
|
48 |
132,045 |
139,897 |
148,216 |
157,029 |
166,366 |
176,259 |
186,740 |
197,844 |
209,609 |
222,073 |
235,278 |
249,268 |
|
49 |
132,121 |
139,978 |
148,301 |
157,120 |
166,463 |
176,361 |
186,848 |
197,958 |
209,730 |
222,201 |
235,414 |
249,412 |
|
Cents |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
|
50 |
132,198 |
140,059 |
148,387 |
157,211 |
166,559 |
176,463 |
186,956 |
198,073 |
209,851 |
222,329 |
235,550 |
249,556 |
Tuning Systems
A tuning system consists of
three components :
(1) SCALAR DIMENSION : the number of steps dividing the octave
:
In Western classical music and also in popular music, the octave is
commonly divided in 12 steps, each step being a semitone.
(2) MASTER TUNING : a standard to tune instruments or concert pitch
;
Before 1711, composers & musicians had no clear reference point to
tune their instruments. Since 1939, an international consensus
exists about concert pitch, with A4 = 440 Hz. This is 8 Hz sharper
than Verdi pitch (A4 = 432 Hz or C3 = 128,434 Hz). Verdi pitch refers to φ (at A4 = 432 Hz, E3 = 161,817 Hz).
The Golden Ratio (φ ≈ 1,618 ...) is also found in the ear as well as
in the harmonic series. In the present study, concert pitch =
Verdi pitch is part of the set of conditions related to the reintroduction of color & natural
harmonic cycles back into music.
(3) SCALAR DEFINITION : the tuning or temperament of the scale.
Defines the interval-relationships between the tones of a
scale.
As the scale stays close to acoustically pure intervals (harmonic, just
intervals), the frequencies of the tones (after which the notes
are named) are related by ratios of two integers. The scale
is "in tune" with the Harmonic Series. Historically, two tunings
stand out : Pythagorean & Just Intonation. The former only
uses the harmonic fifth (3:2), the latter all integer ratios,
introducing limitations as to the complexity of these. So many
variations of Just Intonation exist. But all these tunings generate
a howling wolf interval imposing harmonic limitations. Before the 15th
century, Western music was simple enough to avoid the wolf. With the
Renaissance, these limitations were questioned and eventually left
behind. The wolf had to be eliminated.
To enhance the harmonic capacity
of the scale, i.e. its ability to allow for an increased harmonic
variety, accommodate a wider compositional intent and therefore be
more useful in a broader variety of musical contexts, adjustments
had to be
made to the tones, creating intervals modified (tempered) from their
harmonic, acoustically natural format. In this way, the power of the
wolf diminished or could be rendered nearly harmless. Such tempered intervals are not based on ratios of
two integers. The resulting scale is then called a "temperament"
(because one, some or all intervals are tempered). The later is
therefore a
modification of a tuning, needing radical numbers to express the
ratios of one, some or indeed all of its intervals. In musical practice
today, the commonly used
temperament is Equal Temperament (all semitones beings 50c, a whole
tone 100c and so each step of the 12 steps of the scale 100c, up to
the octave above at 1200c). It is the less natural of all
temperaments !
Barbour (1951), identifying over a hundred historical tunings &
temperaments based
around the octave, categorizes them into five broad groups :
Pythagorean Tuning, Just Intonation, Meantone Temperament, Irregular
Temperament(s) and Equal Temperament.
The
first two are "tunings" (harmonic intervals only), the
last three are "temperaments" (tempered intervals).
a) PYTHAGOREAN Tuning
SCALAR DIMENSION : 12
SCALAR DEFINITION : 3:2 (harmonic fifth) with exclusion rules for
the wolf interval ;
Pythagorean Tuning
defines all the notes & intervals of a scale from a series of perfect
(pure) fifths with ratio of 3:2 = 701,956c, the third harmonic of the
Harmonic
Series (the first two being the fundamental frequency with its
octave). This is easy to tune by ear.
|
TABLE 11 : Pythagorean Intervals |
|
Interval |
Frequency Ratio |
Cents |
|
unison |
1:1 |
0 |
|
minor second |
2187:2048 |
113,686 |
|
major second |
9:8 |
203,910 |
|
minor third |
32:27 |
294,136 |
|
major third |
81:64 |
407,820 |
|
fourth |
4:3 |
498,044 |
|
augmented fourth |
729:512 |
611,730 |
|
fifth |
3:2 |
701,956 |
|
minor sixth |
6561:4096 |
815,640 |
|
major sixth |
27:16 |
905,866 |
|
minor seventh |
16:9 |
996,090 |
|
major seventh |
243:128 |
1109,776 |
|
octave |
2:1 |
1200 |
However, no matter how many
fifths (3/2 intervals) one takes, either above or below a given
note, one never arrives at an exact octave multiple of that
note, but always a discrepancy larger, overshooting the
target pitch, with a ratio of 129,746:128 or 1,013640625:1
instead of 1:1. There are 11 pure fifths and one narrow, out-of-tune
fifth.
3/2 x 3/2 x 3/2 x 3/2 x
3/2 x 3/2 x 3/2 x 3/2 x 3/2 x 3/2 x 3/2 x 3/2 = 531.441/41096 =
129,746
2/1 x 2/1 x 2/1 x 2/1 x
2/1 x 2/1 x 2/1 = 128,0
To tackle this discrepancy, derive a complete chromatic scale taking
a series of 11 perfect fifths. Indeed, no stack of 3:2 intervals fits exactly into any stack of 2:1 intervals (octaves). Take
C, move up 12 fifth and then 7 octaves down. This brings one to B#,
almost exactely where one started. The crucial discrepancy is the
small interval (or comma) existing in Pythagorean tuning between two
enharmonically equivalent notes such as C and B# (or Ab and G#). It
is equal to the frequency ratio 312/219 =
531441:524288 (= 1,013643265 ...). Log2 (1,013643265) =
0,01955 x 1200 = 23,46c ; the Pythagorean comma or ditonic comma.
"Now if one continues indefinitely adding
fifths in an upward direction (setting up the circle of fifths), one
is headed for infinity, for with the twelfth fifth a tone is reached
which is also a comma higher than the octave of the original tone.
(...) The ear is easily reconciled to impure fifths, if the
discrepancy is very slight, as the equally tempered scale shows ;
but it would not accept impure octaves." -
Hindemith
(1942, Book 1, p.31).
Suppose we tune in D,
then we first move six times a ratio 3:2 up : D - A - E - B - F# -
C# - G#. We generate the the six other notes of the chromatic scale
by moving six times a ratio 3:2 down : Eb - Bb - F - C - G - (D). If
we add one more note to this stack, we arrive at : Ab - Eb - Bb - F
- C - G - D - A - E - B - F# - C# - G#. This is very similar, but
not exactely identical in size to a stack of 7 octaves. Indeed, it
is a Pythagorean comma larger.
Therefore,
Ab and G#, when brought into the basic octave, will not coincide as
expected. To get around this problem, the chromatic Pythagorean
scale ignores Ab, and uses only the 12 notes from Eb to G# (C# but
not Db, F# but not Gb, G# but not Ab, Bb but not A#, Eb but not D#).
So only 11 perfect fifths are used to build the entire chromatic
scale. The remaining fifth (from G# to Eb) is left out-of-tune ! So
music combining those two notes is unplayable in this tuning. This
very out-of-tune interval is the wolf interval (the 11
perfect fifths are 701,956c wide, in the exact ratio 3:2, except the
solitary wolf fifth, which is only 678,495c wide = 701,956c -
Pythagorean comma).
|
TABLE 12 : The Pythagorean Scale |
|
C |
C# |
D |
Eb |
E |
F |
F# |
G |
G# |
A |
Bb |
B |
C |
|
1:1 |
2187:2048 |
9:8 |
32:27 |
81:64 |
4:3 |
729:512 |
3:2 |
6561:4096 |
27:16 |
16:9 |
243:128 |
2:1 |
|
0c |
114 |
204c |
294c |
408c |
498c |
612c |
702c |
816 |
906c |
998c |
1110c |
1200c |
In the case the notes G#
and Eb need to sound together, the position of the wolf fifth
can be changed. For example, a C-based Pythagorean tuning would
produce a stack of fifths running from Db to F#, making F# - Db the
wolf interval. As there is always one wolf fifth in Pythagorean
tuning, playing all keys in tune is impossible.
In music not changing key very often, or not very harmonically
adventurous, the wolf interval is unlikely to be a problem, as not
all 12 fifths will be heard in such pieces. Because 11 fifths in
Pythagorean tuning are in the simple ratio of 3:2, they sound very
"smooth" and "consonant". The thirds, by contrast, with relatively
complex ratios of 81:64 (for major thirds) and 32:27 (for minor
thirds), sound less smooth. Pythagorean tuning is particularly well
suited to music which treats fifths as consonances, and thirds as
dissonances. In the West, this means music written prior to the 15th
century.
b) JUST Intonation (or
Just Tuning)
SCALAR DIMENSION : 12
SCALAR DEFINITION : always pure, harmonic intervals, possibly simple
integers ;
Just Intonation is also
based on the harmonic series, i.e. makes use of acoustically
beatless intervals. Compared with Pythagorean Tuning (only using
3:2), Just Intonation arrives at other frequency ratios for the
intervals.
|
TABLE 13 : Just Intonation (7-limit) |
|
Interval |
Frequency Ratio |
Cents |
|
unison |
1:1 |
0 |
|
minor second |
16:15 |
111,731 |
|
major second |
9:8 |
203,910 |
|
minor third |
6:5 |
315,641 |
|
major third |
5:4 |
386,314 |
|
fourth |
4:3 |
498,044 |
|
augmented fourth |
7:5 |
582,513 |
|
fifth |
3:2 |
701,956 |
|
minor sixth |
8:5 |
813,686 |
|
major sixth |
5:3 |
884,359 |
|
minor seventh |
9:5 |
996,090 |
|
major seventh |
15:8 |
1088,269 |
|
octave |
2:1 |
1200 |
Various systems of Just
Intonation were designed. Usually, a limit is imposed on how complex
the ratios used in Just Intonation are. Just Intonation 7-limit
implies there is no prime number larger than 7 featuring in the
ratios.
|
TABLE 12 : Basic Just Intonation (7-limit) |
|
C |
Db |
D |
Eb |
E |
F |
F# |
G |
Ab |
A |
Bb |
B |
C |
|
1:1 |
16:15 |
9:8 |
6:5 |
5:4 |
4:3 |
7:5 |
3:2 |
8:5 |
5:3 |
16:9 |
15:8 |
2:1 |
|
0c |
112 |
204 |
316 |
386 |
498 |
583 |
702 |
814 |
884 |
996 |
1088 |
1200c |
Wolf intervals also
occur and hence the same problems as with Pythagorean Tuning
persist.
c) MEANTONE Temperament
SCALAR DIMENSION : 12
and more
SCALAR DEFINITION : various attempts to make the major third pure by
tempering the fifths, with no circularity ;
The first temperaments
date from the 15th century, while the earliest discussions happened
a century earlier. The exclusive use of the perfect fifth
(Pythagorean) or other harmonic intervals (Just Intonation), causing
a wolf interval, limited the harmonic possibilities of composers &
musicians. The major thirds in Pythagorean were too wide and the
minor thirds too narrow.
|
TABLE 13 : Harmonic, Pythagorean & Just
Intonation Thirds |
|
Pythagorean Major Thirds |
Pythagorean Minor Thirds |
Just Intonation Major Thirds |
Just Intonation Minor Thirds |
Harmonic Major Thirds |
Harmonic Minor Thirds |
|
407,820c (81:64) |
294,136c |
386,314c |
315,641c |
386,314c (5:4) |
315,641c |
In Meantone Temperament,
the whole tone is precisely half of the harmonic major third
(386,314c/2 = 193,157c). It rejects the wide Pythagorean third and
seeks to establish the harmonic major third by tempering certain
fifths. Eventually, Meantone Temperament sought to "close" the
circle and eliminate the wolf interval. The wolf remained.
The idea underlying Meantone Temperament was to make the major third
as acoustically pure as possible. However, in a twelve-note
octave, a circle of pure major thirds does not fit in (three pure
major thirds = 5:4 x 5:4 x 5:4 = 125/64 or 1,953:1 instead of 2:1).
In the Renaissance this was not really a problem, because composers
did not use all the major thirds. Moreover, they did not notate
music with more than two flats, and rarely with sharps.
To make the thirds sound good, the fifths were narrowed (the
harmonic fifth of 701,956c became the meantone fifth of 696,57843 in
1/4-comma or 698,3710 in 1/6-comma). This was the disadvantage of
this system. But in combination with perfect euphonious thirds,
these tempered fifths were tolerable.
To achieve acoustically pure major thirds, four consecutive fifths
in the circle were tempered by one-quater of the difference between
Pythagorian and pure major thirds. This difference of 21,506c
(407,820c - 386,314), with ratio 81:80 (21,5064c) is called the
syntonic comma, diatonic comma or Ptolemaic comma. This is the
temperament know as "quater-comma" Meantone. Here we have eight pure
thirds and four thirds which are really diminished fourths. The
syntonic comma was spread over four fifths.
|
TABLE 13 : 1/4-comma Meantone Temperament
(Piertro Aaron - 1523) |
|
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
C |
|
0c |
76 |
193 |
310 |
5:4 |
503 |
579 |
697 |
25:16 |
890 |
1007 |
1083 |
1200 |
In the 16th century, it
was suggested to spread the comma over five or six fifths, causing
less differentiation between the four "bad" thirds. The eight "good"
thirds (393c) were no longer harmonic thirds (386c), but sounded
good while the fifths were better. These are the one-fifths or
one-sixth-comma Meantone Temperaments.
In none of these systems was the wolf interval eliminated, and so
the 24 keys were not all available (some chords sounding
out-of-tune). But in all of them the harmonic fifth & major third
were prominent.
"The strongest, most unambiguous interval,
after the octave, which is unique, is the fifth, while the most
beautiful is the major third, on account of the triad formed by it
with its combination tones." -
Hindemith
(1942, Book 1, p.88). For Hindemith, "the
frequency of the combination tone is always equal to the difference
between the frequencies of the directly produces tones of the
interval" (p.61).
|
TABLE 14 : 1/6-comma Meantone Temperament
(Salinas) |
|
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
C |
|
0c |
89 |
197 |
305 |
393 |
502 |
590 |
698 |
787 |
895 |
1003 |
1092 |
1200 |
d) IRREGULAR Temperaments
SCALAR DIMENSION : 12
SCALAR DEFINITION : combinations of pure & tempered major thirds &
fifths eliminating the wolf ;
With the discovery all
fifths did not have to be tempered the same amount, a new group of
temperaments emerged. These "irregular" temperaments mixed
different
amounts of tempering and so called for different sizes of fifths &
thirds. By this adjustment, mixing harmonic & tempered fifths, the
wolf interval could be driven out (closed temperaments) and more
chords created. This assisted composers who intended to write
chromatic lines and complexer harmonies (with sharp & more than two
flat signatures), like diminished and seventh
chords. The idea was to make all 24 keys around the circle of fifths become available
(circular temperaments). All the notes & chords of the set of 12 major & 12 minor
keys sounded "well" together ! The
tirany of the wolf interval, limiting full harmonic expression, had
ended. A harmonic logic with more categories & rules could be
invented.
If the studies of
Lehnman are correct, Johan Sebastian Bach was the first composer
to musically acknowledge the crucial importance of this in his Das Wohltemperierte Klavier (BWV
846–893). The word "wohl" does not refer to "equal", but to the
euphonous qualities of the 24 tonal scales in Bach's irregular
temperament. Because of the variety of intervals within these irregular temperaments, each key
had its own harmonic characteristics or "key color". Indeed, the
flavor of the chords was slightly different in each key. Bach's
temperament keeps C, D, E, F, G & A in evenly-spaced positions, at
their normal place within the context of late 17th century practice.
Then six remaining notes (B and the sharps F#, C#, G#, D# & A#) are
put in place with adjustments making them also serve well as flats.
A staggering variety of irregular temperaments saw the light, each
temperament having its own advantages and disadvantages. Some
favored certain chords & keys, while others did not sound well.
Or they sounded more or less all good, but were very difficult to
tune. In the tuning world, some of these systems are known under the
name of their inventor : Andreas Werckmeister, Johann Philipp
Kirnberger, Johann Georg Neidhardt, Antonia Vallotti, Thomas Young
and many others.
Two outstanding irregular temperaments : Johan Sebastian Bach and
Thomas Young, both giants in their field. According to
Murray Barbour, Young's temperament is "the best
of these many irregular systems" (Barbour,
1951, p.12)
|
TABLE 15 : Lehman - Bach Temperament |
|
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
C |
|
0c |
98,045 |
196,09 |
298,045 |
392,180 |
501,955 |
596,090 |
698,045 |
798,045 |
894,135 |
998,045 |
1094,135 |
1200c |
Irregular temperaments
always leave certain fifths untempered. For example, in Young's
temperament n°2, a superb example of simplicity & elegance, 6 fifths (C - G - D - A - E - B - F#) are
tempered by 1/6 of a Pythagorean comma, while the 6 others remain
harmonical (pure, beatless, acoustically perfect).

Thomas Young's
Well Temperament (N°2)
inside : tempering of each fifth
outside : tempering of each third
inside triangle : combined tempering of each triad
Young N°2 starts
the set of tempered fifths with C as "scalar center", making the key of C# (Db) beat
the most and the key of G the less. If the scale would start with F, F# (Gb)
would be the worst and C the best, etc. The fifth (for example : C
- G) is tempered with 1/6th of a Pythagorean comma (or 23,460c/6 =
3.910c), or a perfect fifth (3:2) of
701,956c - 3.91c = 689.046c.
|
TABLE 16 : Thomas
Young Temperament N°2 (1/6-comma - 1807) |
|
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
C |
|
0c |
256:243
90.224 |
195,09 |
32:27
294.134 |
392,18 |
4:3
498.044 |
1024:729 |
698,045 |
128:81
588.270 |
894,135 |
16:9
996.090 |
1090,225 |
1200c |
Young N°2 defines the
minor third harmonically (32:27).
"What then, is the minor triad, in reality ? I
hold, following a theory which again is not entirely new, that it is
a clouding of the major triad. Since one cannot even say definitely
where the minor third leaves off and the major third begins, I do
not believe in any polarity of the two chords. They are the high and
low, the strong and weak, the light and dark, the bright and dull
forms of the same sound." -
Hindemith
(1942, Book 1, p.78).
"Again we may say that Young's version is an excellent irregular
temperament ..." (Barbour,
1951, p.181). The trouble with these mathematically excellent
systems
"is that they are too good !" (Ibidem, p.178). The step from "paper" to
"practice" is difficult and
involves hearing the beats of the beating fifths.
In our age, assisted by electronics, tuning & retuning has become a
mere preset.
d) EQUAL Temperament
SCALAR DIMENSION : 12
SCALAR DEFINITION : tempering all intervals alike, no pure
intervals, no color, no wolf ;
Already known in
Antiquity (Aristoxenus in the 4th century BCE), who preferred
another system, Equal Temperament became an issue around 1640, if not
earlier. The father of Galileo Galilei (Vincenzo) advocated the
system and composed dance suites on each of the notes of the
chromatic scale (in all keys).
The octave (of 1200c)
is divided into 12 of 100c and a whole tone divided in
two semitones of 50c each.
The scale is constructed by way of 2n/12
(n = 1 for C -unison- and n = 12 for C' -octave-). All steps are
tempered by 1/12 of a Pythagorean comma, or 23.46/12 = 1.96 cents.
In the past, theorists as wel as musicians found Equal Temperament coarse, disagreeable (Thomas Smith), with
a beating heightening emotion (Johann Neidhardt).
"... the ear is subject to a certain danger in
being exposed only to music constructed of tempered intervals ; it
accustoms itself to their clouded qualities, and like a jaded palate
loses its sense of natural relations." -
Hindemith
(1942, Book 1, p.28).
In Equal
Temperament, major thirds (400c) are far too wide compared to the
harmonic major third (386,314) and minor thirds (300) too small
compared to the harmonic minor third (315,641), creating an
unpleasant, coarse "beat".
In all previous
systems, the tone (of 9 commas) had been divided in a minor (4
commas) & a major (5 commas) semitone. This was abolished. The
relationship maintained between the Harmonic Series was also
eliminated. Each step of the scale is tempered. Hence, except
for the octave, no acoustically pure intervals remain ! This means
this temperament breaks with the underlying acoustical
phenomena. This scale moves too far away from natural law to allow
for color. This is the dictate of unnaturalness. The uniform intervals lack expressive
variety, making the 24 keys loose their characteristic harmonic
"coloration". Keys are merely shades of gray.
|
TABLE 17 : Equal
Temperament |
|
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
C |
|
0c |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
1100 |
1200c |
The advantage of this
temperament is easy tuning and standardisation, but the cost is loss
of harmony, or as some rightly claim, the "ruin" of harmony as such
...
In terms of the Farben Project, tempering all intervals except the
octave means the end of coloration and this is precisely the
opposite of its intent. It wants to generate color.
This calls for the following tuning system :
(1) scalar dimension : the division of the octave in 12 steps ;
(2) master tuning : Verdi Pitch (A4 = 432 Hz) ;
(3) scalar definition : all tunings & temperaments are possible and
should be used as a function of the music in
question. Young N°2 is the best temperament. Equal Temperment is a default accommodating
standardisation. It is the worse.
§ 8 Psycho-Acoustic
Definitions
The impact of music on
the human being, besides auditive input, is mainly through resonance, the vibration imparted
on the psycho-biological system as a result of sound waves from one
or more sources of sound, if possible musical instruments. These resonances happen all through the
body. If these vibrations are in harmony with
the laws of acoustics (in terms of the harmonic series and the
φ-base of human hearing), then this impact is wellness, or
beatlessness. If, due to the beating between the overtones of these
sound waves, pure vibes cannot be maintained, a disturbing
resonance is at hand. In louder form this becomes auditive
pollution.
Psycho-acoustics aims to entrain the listener by way of sound waves
most likely to trigger the natural restoring response of a system
vibrating in tune with the acoustics of the harmonic series, the
human ear and color.
"When a stimulus reaches the visual cortex, a
visual evoked response is produced, a response that follows the
frequency characteristic of the stimulus." (Evans,
2007, p.251.)
This brings the visual into the equation,
opening the way for combining music & color during performance
(Scriabin, the color organ). Eventually, this may lead to an individualized
& audio/visually scripted entrainment, a session running HRV
feedback & EEG-driven (like Mind Work Station & Bioexplorer), with parameters set to specific targets.
How to find a series of plausible Psycho-Acoustic criteria ? On the
basis of my various
hermeneutical studies on religious language & practice,
provisional "esoteric" tables of correspondences can be put together
(cf.
Tabula Tabularum Esotericum, 2006).
Of these various
correspondences, let us analyze the relationships proposed between
the energy-wheels of the subtle energy-body (in Taoism, Hinduism &
Buddhism), states of yogic consciousness (in Classical Yoga) and the
symbolic language of the Qabalah (with its numerical, astrological,
alchemical and psycho-dynamic semantic charts). Especially the
Chakra's (energy-vortices) are interesting, for there are seven main
energy-fields, each associated with a spectral color. These wheels
also associate with certain functions, cognitive modes and proposed
brain frequencies.
|
TABLE 18 : Defining Provisional Psycho-Acoustic
Criteria |
Wavelengths of Visible Spectrum
(in nm) |
Centres of Color Gravity |
Tone Names
Middle C = C4 |
Verdi
Pitches
(in Hz) |
QBL |
Chakra |
Subtle Bodies |
Function |
Cognitve
Modes |
Brain frequency |
|
VII VIOLET |
400 to 380 |
390 |
G4 |
384,868 |
1 Ur |
crown |
monadic |
unity
selflessness |
nondual |
Gamma
+ 90 Hz |
|
Dark Blue |
420 to 400 |
410 |
G#4
Ab4 |
407,754 |
2 Ne |
|
|
|
|
|
VI BLUE |
450 to 420 |
435 |
A4 |
432 |
brow |
logoic |
insight
awareness |
Gamma
+ 50 Hz |
|
Light Blue |
475 to 450 |
462,5 |
A#4
Bb4 |
457,688 |
3 Pl |
throat |
buddhic |
language
speech |
Gamma
+ 40 Hz |
|
V CYAN |
495 to 475 |
485 |
B4 |
484,904 |
|
|
|
|
|
IV GREEN |
520 to 495 |
507,5 |
C5 |
513,737 |
4 Ju
6 Su |
HEART |
causal |
integration
compassion
higher self |
creative |
Beta+
21/32 Hz |
|
Yellow Green |
565 to 520 |
542,5 |
C#5
Db5 |
544,286 |
5 Ma
8 Me |
|
mental |
|
critical |
Beta-
13/21 Hz |
|
formal |
Alpha+
10/13 Hz |
|
III YELLOW |
575 to 565 |
570 |
D5 |
576,651 |
navel |
thought
will, ego |
imitative |
Alpha-
8/10 Hz |
|
Yellow Orange |
615 to 575 |
595 |
D#5
Eb5 |
610,94 |
7 Ve
9 Lu |
|
astral |
|
tribal |
Theta
4/8 Hz |
|
II ORANGE |
645 to 615 |
630 |
E5 |
647,269 |
sacral |
drives, emotions feeling affect |
|
I RED |
720 to 645 |
682,5 |
F5 |
685,757 |
10 Sa |
root |
etheric |
instinct, survival |
libidinal |
delta
1/4 Hz |
|
Dark Red |
750 to 720 |
735 |
F#5
Gb5 |
726,535 |
|
physical |
|
These correspondences
may be used to compose music intended to have psycho-acoustic
effects. The question then is : How to translate the criteria into
an intented effect and this into a piece of music ? |